addition
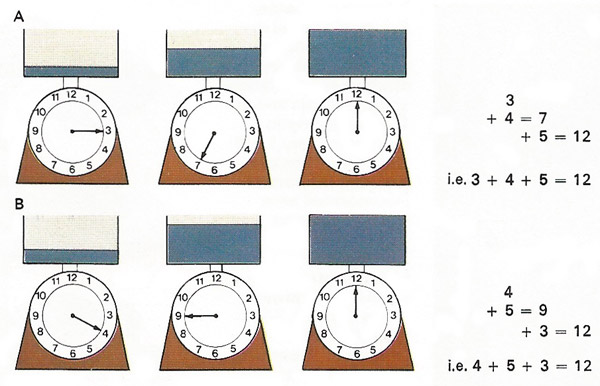
Addition is associative – that is, a series of additions can be carried out in any order without affecting the result. This diagram shows the effects of successively weighing [A] 3, 4, and then 5 units of a substance on a spring balance and [B] weighing 4, 5, and then 3 units. In both cases the total weight – the sum or the additions – is 2 units. As in many other mathematical laws, this is applied common sense.
Addition is one of the four fundamental operations of arithmetic. It is denoted by the sign '+'.
The numbers that are added are called terms, addends, or summands. For example, 4 (an addend) + 3 (another addend) = 7 (sum).
Addition of fractions
Fractions can be added directly only if they have equal denominators, e.g., 3/17 + 4/17 = 7/17.
If fractions with unequal denominators are to be added they must first be brought to their least common denominator.
Addition of literal numbers
Identically-named numbers can be added (and subtracted) by adding the coefficients:
2a + 3b + a + 4b = 3a + 7b
summands may be interchanged (commutative law):
a + b = b + a
With more than two summands, brackets may be inserted (associative law):
a + b + c = (a + b) + c = a + (b + c)
Addition of directed numbers
No further rule is needed for the addition of positive numbers:
a + (+b) = a + b, 5 + (+3) = 5 + 3 = 8.
to add one negative number to another, its absolute value is subtracted:
a + (–b) = a – b, (–a) + (–b) = –(a + b);
5 + (–3) = 5 – 3 = 2, (–5) + (–3) = –(5 + 3) = -8.
Addition of powers and surds
Powers and surds must be treated like literal numbers for the purposes of addition, e.g.,
a 2 + 4b 3 + 4c 3 +4a 2 = 5a 2 + 4(b 3 + c 3;
3√2 + 5√3 + √2 = 4√2 + 5√3
Addition of complex numbers
In adding complex numbers the real and imaginary parts must be added separately, e.g.,
(5 + 3i) + (17 – i) = 22 + 2i.
Addition in terms of sets
The addition of positive numbers can best be defined in terms of set theory; if one considers set A to contain 4 elements, set B to contain 5 elements, then A U B (see union) contains 9 elements; i.e., 4 + 5 = 9. The addition of negative numbers is equivalent to subtraction in that a + (–b) is equivalent to a – b.


