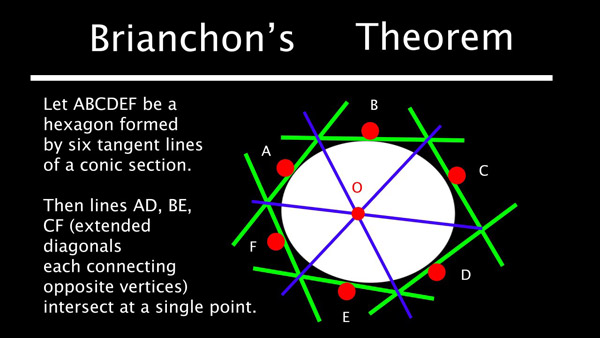
Brianchon's theorem states that given a conic section, if we circumscribe a hexagon about it (see circumscription), then the three major diagonals of the hexagon are concurrent (i.e. meet at a point). It is named after the French mathematician Charles-Julien Brianchon (1783–1864) who published the theorem in 1806 while he was still a student. In fact, Brianchon's theorem is simply the dual of Pascal's theorem which was proved in 1639. After graduation, Brianchon became a lieutenant in the artillery fighting in Napoleon's army until he left active service in 1813 due to ill health. His last work in mathematics made the first use of the term nine-point circle. By 1823, Brianchon's interests turned to teaching and to chemistry