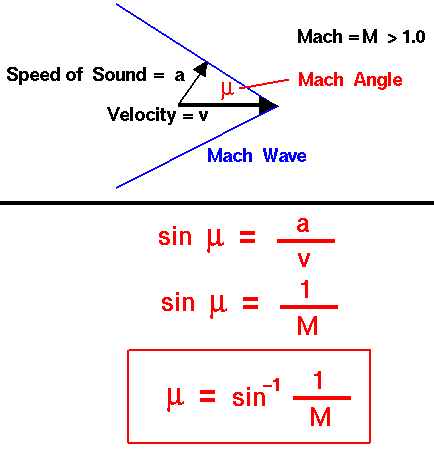
The Mach angle is the angle a shock wave makes with the direction of motion as determined by the velocity of the object and the velocity of shock propagation.

 

As an object moves through a gas, the gas molecules are deflected around the object. If the speed of the object is much less than the speed of sound of the gas, the density of the gas remains constant and the flow of gas can be described by conserving momentum, and energy in the flow. As the speed of the object increases towards the speed of sound, we must consider compressibility effects on the gas. The density of the gas varies locally as the gas is compressed by the object. Near and beyond the speed of sound (about 330 meters per second or 700 mph on Earth at sea level), small disturbances in the flow are transmitted to other locations isentropically (with constant entropy) as sound waves.

 

For supersonic and hypersonic flows, small disturbances are transmitted downstream within a cone. The edge of the cone is depicted two-dimensionally by the blue lines in the figure. The sound waves strike the edge of the cone at a right angle and the speed of the sound wave is denoted by the letter a. The flow is moving at velocity v which is greater than a. From trigonometry, the sine of the cone angle μ is equal to the ratio of a and v:

 

    sin(μ) = a/v

 

But the ratio of v to a is the Mach number of the flow.

 

    M = v /a

 

With a little algebra, we can determine that the cone angle μ is equal to the inverse sine of one over the Mach number.

 

    sin μ = 1/M

 

    μ = sin^–1(1 M)

 

where sin^–1 is the inverse sine function. μ is an angle which depends only on the Mach number and is therefore called the Mach angle of the flow.

 

We are interested in determining the Mach angle because small disturbances in a supersonic flow are confined to the cone formed by the Mach angle. There is no upstream influence in a supersonic flow; disturbances are only transmitted downstream within the cone.