reactance (X)
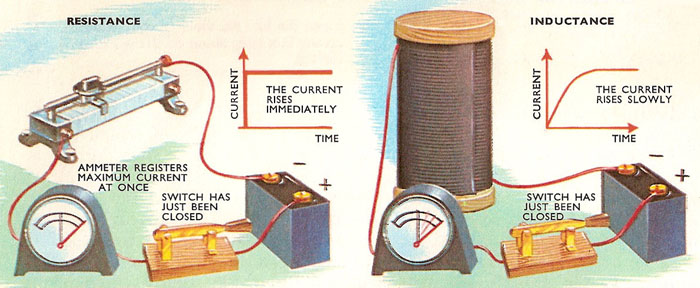
A direct current connected across a resistance rises immediately when the switch is closed. But the current through an inductance rises slowly. Whenever the current in a coil of wire changes, a current is generated in the opposite direction, if it has a complete circuit to flow around.


Reactance (X ) is a property of an AC circuit containing capacitance or inductance that together with any resistance makes up its impedance. The impedance Z is given by Z 2 = R 2 + X 2, where R is the resistance and X is reactance. For a pure capacitance C, the reactance is given by XC = 1/2πfC, where f is the frequency of the alternating current; for a pure inductance L, XL = 2πf L. If resistance, inductance, and capacitance are in series the impedance Z = √[R2 + (XL – XC)2]. Reactance is measured in ohms.
Chokes and inductive reactance
Switch a battery across a resistance, and the current in the circuit immediately jumps to its full value (which of course depends on the voltage supplied by the battery and the resistance in the circuit according to Ohm's law). But replace the resistance with a choke (a large coil of wire), and the current rises gradually to its full value, again determined by the resistance of the coil. Some property of the coil resists the change in current. This property is the inductance, and the "resistance" of the coil to changing currents is the inductive reactance.
When a current flows through a wire it sets up a magnetic field around the wire. As the current rises or falls, the magnetic field rises or collapses, i.e., it is a moving field. When the wire is coiled into a series of loops the magnetic field around one loop cuts some of the other loops. Whenever moving magnetic fields cut wires, they generate a difference in electric pressure (i.e., an electromotive force or e.m.f.) which pushes a current through the wires, provided the current has a complete circuit to flow around. This is one of the two fundamental principles of electromagnetism – the generator principle. In the electric generator a moving coil rotates through a steady magnetic field and makes a current flow in the wire. A steady field on a moving coil has the same effect as a moving field on a steady coil – the generation of a current.
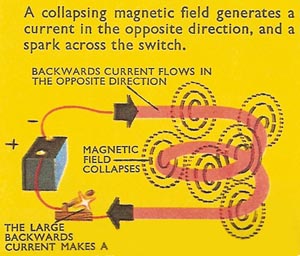
So as soon as a current starts to flow round the coil, it makes a growing magnetic field, which generates another separate current. The generated current could flow in either of two directions – in the same direction as the current from the battery or in the opposite direction. If it flowed in the same direction, it would increase the field around the coil, which would generate a bigger current in the adjacent coils, and the process would repeat itself, the current rapidly increasing without limit.
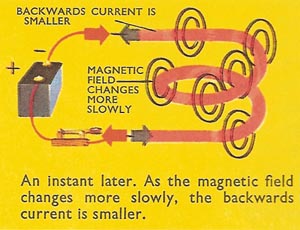
But this is not what we see when the battery is switched across the coil. In fact, the current slowly builds up to a steady maximum. So the current must flow in the opposite direction, and tends to reduce the total current in the coil. The backward current is never as large as the forward current from the battery, which must win in the end. As the current approaches its maximum value, it changes more slowly and the back e.m.f. and the backward current are therefore smaller. When the magnetic field is steady there is no backward current at all.
The more turns of wire there are in the coil the more turns each turn can affect, or the greater the coil's inductance. Its inductive reactance – the resistance-to-change it offers – is greater.
Inductance affects a DC circuit only when the current is switched on and switched off. Alternating current, on the other hand, is changing its direction, to-and-fro, all the time. The more rapidly the current changes, the more rapidly the magnetic field it makes changes, and the greater will be the inductive reactance which tries to slow down the change.


