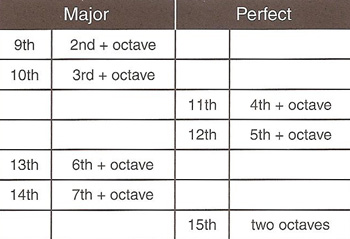
A compound interval is an interval that is greater than an octave. Compound intervals are named ninth, tenth, eleventh, twelfth, and so on. They can be considered equivalent to their counterparts an octave lower, which are called simple intervals. The ninth interval, for instance, is a compound second (a second plus an octave) and is likewise major in quality.

 

Compound intervals do not obey the rules of normal arithmetic. Ordinarily, 8 + 5 = 13 but adding a fifth to an octave gives not a thireteenth but a twelfth. This is because the note at the top of the octave is repeated as the note at the bottom of the fifth. We only need to include it once in the compound interval of a twelfth.

 

Compound intervals can have all the qualities (diminished, minor, major, augmented, perfect) encountered with smaller intervals.

 

The tenth and twelfth are harmonically like the third and fifth, respectively, of a triad. However, the ninth, eleventh, and thirteenth don't correspond to any intervals in a triad. See also extended chord.