speed and velocity

Figure 1. Speed is the rate of change of position of an object with time, while velocity is the rate of change of position in a particular direction. These arrows represent a group of objects moving at the same speed, but only two have the same velocity.
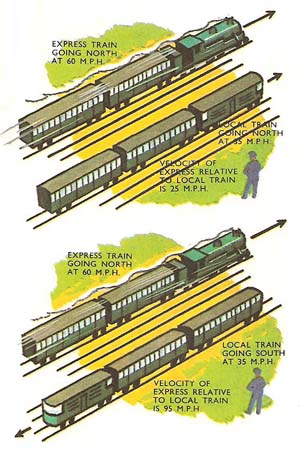
Figure 2. When both trains are going in the same direction (north), the velocity of the faster train at 60 mph relative to the slower train (35 mph) is 25 mph in a northerly direction. However, if the slower train were going south, the relative velocity of the faster train is 95 mph.

Figure 3. While a passenger remains seated his velocity is the same as the ship's (15 knots), but when he moves forward his velocity relative to the jetty is greater (18 knots).
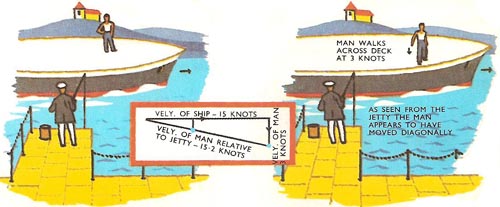
Figure 4. If he walks across the deck, he follows a diagonal path as viewed from the jetty. His velocity relative to the jetty can be found from the triangle of velocities.
The words "speed" and "velocity" are often used in everyday language as if they mean the same thing – how fast something is moving. But in physics these words don't mean the same thing at all. To a physicist, speed is how fast something is moving but velocity is how fast something is moving in a particular direction (see Figure 1). For example, if you say that a car is moving at 60 miles an hour, that's it's speed. But if you say that the car is moving north at 60 miles an hour then you've given it's velocity. Physicists call speed a SCALAR, which means its a quantity that only has magnitude (size). Velocity, on the other hand, is a VECTOR, which means it has both magnitude and direction.
Relative velocity
Two trains are standing beside one another in a station and one starts to move. A passenger in one train thinks it is his train that is moving. Certainly he seems to be moving past the windows and doors of the carriages of the other train. Suddenly he turns to look through the opposite window and, to his surprise, finds that his window is still opposite the door of the refreshment room on the station platform. His train is still standing in the station so it must have been the train standing at the next platform that has departed in the opposite direction.
Many railway passengers must have experienced this rather strange sensation at one time or another. Although at first the passenger thinks the train is moving, he can only really be certain that one train is moving in relation to the other. But a porter standing on the platform knows which is moving because he is stationary and can tell when either objects are moving.
For velocity to have any meaning at all it must be measured in relation to some reference point. This reference may be stationary or may itself be moving. For instance, an express train appears to be moving much faster to some standing beside the track than to a passenger in a slow moving train traveling in the same direction alongside the express.
The stationary observer and the moving passenger get different results when they measure the velocity of the express train because of the difference in their own velocities. If no reference is mentioned, it is normal to assume that all velocities are measured with reference to the stationary ground. Velocities measured from a moving observation point are called relative velocities, but to avoid confusion in problems concerning moving objects, the velocity of the observer or the position of the observation point should always be stated.
Perhaps a stationary bystander sees a faster train traveling north at a velocity of 60 mph and a slower train traveling alongside in the same direction at 35 mph. (These are the velocities relative to the ground.) But to someone in the slower train, the faster one appears to be moving north at only 25 mph. The velocity of the faster train relative to the slower one is 25 mph in a northerly direction (see Figure 2).
The two trains are moving along parallel paths, and it is an easy matter to calculate the velocity of one relative to the other, provided their velocities relative to the ground are already known. For instance the velocity of the faster train relative to the slower one was found by subtracting their respective velocities (60 - 35 = 25 mph). The velocity if the slower train relative to the faster one is 35 - 60 = -25 mph. The minus sign here indicates that to someone in the faster train the slower train appears to be going backwards. It has a relative velocity of 25 mph in a southerly direction.
If instead, the two trains were moving in opposite directions (the slower train going south and the faster train north) the velocity of one relative to the other is found by adding together the speeds of each relative to the ground. (This is the same as subtracting their velocities, because they are heading in different directions. The velocity of one will be negative and subtracting a negative number is the same as adding a positive number.)
To someone on the slower train heading south, the faster train seems to be rushing northward at 95 mph (60 + 35). The passengers in the faster train think the same thing about the slower train, only to them it appears to be heading southward.
These trains have been running on parallel tracks and the relative velocity problems concerning them are quite simple. But a ship has no such lines to guide its path and can be steered in any direction. Consequently, the problems connected with relative velocities of ships are more complicated.
If the ship is moving forward at 15 knots (a knot is a speed of one nautical mile per hour), and a passenger is sitting in a deck chair (i.e. he is stationary relative to the ship) he, too, will be moving forward at 15 knots relative to an observer on a nearby jetty. (We're assuming that the effects of winds and currents can be neglected.)
If the man now gets up and walks forward with a velocity of 3 knots, the observer sees him moving at 18 knots – the passenger's velocity relative to the ship (3 knots) plus the ship's velocity relative to the observer (15 knots). But if, instead, the passenger walked across the port (left) side to the starboard (right) side of the deck at 3 knots, the observer on the jetty would see him taking a diagonal path. While the passenger on the deck was crossing the deck at 3 knots relative to the ship, the ship was carrying him forward at 15 knots relative to the observer on the jetty (see Figures 3 and 4).
The actual velocity of the passenger relative to the observer on the jetty may be found by drawing a triangle of velocities. One side of the triangle is drawn to represent in size and direction the velocity of the ship relative to the jetty – the line is drawn 15 units long to represent the speed of 15 knots. This shows where the passenger would have been, had he not walked across the deck (i.e., had remained in one place on the deck). From the end of this line another line is drawn at right-angles to represent in size and direction the velocity of the man. This second line is only 3 units long to represent the passenger's velocity of 3 knots relative to the ship. The triangle is then completed by drawing in the third side. This line represents in size and direction the velocity of the passenger relative to the observer on the jetty. The size of the velocity can be found by measuring the length of the line.
Cross winds and currents can send a ship miles off course if no allowance is made for them. However, by similar reasoning to the above the effects of wind and current on the course of a ship can be found and in setting course allowance is made for them. If this is done correctly the ship should arrive safely in port.
Units of speed
In the section above, we used miles per hour (mph) and knots as units of speed. To write a value of speed in science we usually use the units m/s (meters per second) or km/h (kilometers per hour). You may also see the value of speed given in other units, such as m/min (meters per minute) or km/s (kilometers per second). Are these notations wrong? Don't worry, these notations are also correct. We just need to know how to change from one form of unit into another.
First, let's look at the basic units of time and distance we're working with:
1 hour (1 h) = 60 minutes (60 min) = 3,600 seconds (3,600 s)
1 minute (1 min) = 60 seconds (60 s)
1 second (1 s) = 1/60 of a minute = 1/3600 of an hour
1 kilometer (1 km) is equal to 1,000 meters
1 meter (1 m) = 1/1000 of a kilometer
1 meter (1 m) is equal to 100 centimeters (100 cm)
1 cm = 1/100 of a meter
OK, now it's time to solve this riddle by using the simple example.
Convert this value: 72 km/h
to m/s (meters per second).
72 km/h = 72 × (1000 m)/(3600 s) = (72 × 1000 m)/(3600 s) = (72000 m)/(3600 s) = 20 m/s.
As you can see it was not so complicated, right?
And now let's do the same, but from another side.
Convert this value: 20 m/s
to km/h (kilometers per hour).
20 m/s = 20 (1/1000 km)/(1/3600 h) = (20 × 1/1000 km)/(1/3600 h) =
(20/1000 km)/(1/3600 h)
= (20 km/1000) × (3600/(1 h)) = 72 km/h
Don't worry, it only looks complicated!
All the essential knowledge needed to perform these calculations consists of a simple mathematical operations, and knowledge of units of length and time.
As you can see it is much easier to convert km/h to m/s than vice versa, but both can be performed.
Now let's deal with these two.
(a) Convert this value: 30 m/min
to km/h.
30 m/min = 30 × (1/1000 km)/(1/60 h) = (30/1000 km)/(1/60 h) = (30
km/1000)(1/60 h)
= (30 km/1000)/(1/60 h) = (30 km × 60)/(1000 × 1 h) = (1800 km)/(1000
h) = 1.8 km/h.
(b) Convert this value: 45 km/min
to cm/s
45 km/min = (45 × 1000 m)/(60 s) = (45 × 1000 × 100 cm)/(60 s) = (4500000 cm(/(60 s) = 75,000 cm/s
Now something to move your imagination:
Two F1 racing cars are competing to be first across the finish line. The speed of the first F1 racing car is 100 km/h; the speed of the second F1 car is 100 m/s. Which car will be first to reach the finish line?
Let v1 be the speed of first F1 car and v2 the speed of the second car.
Convert 100 km/h to m/s.
100 km/h = 100 × (1000 m)/(3600 s) = (100 × 1000 m)/(3600 s) = (100000 m)/(3600 s) = 27.78 m/s.
Now we are able to compare these two values:
v1 = 27.78 m/s
v2 = 100 m/s
v1 < v2
The conclusion is simple: the second F1 reaches the finish line first.
