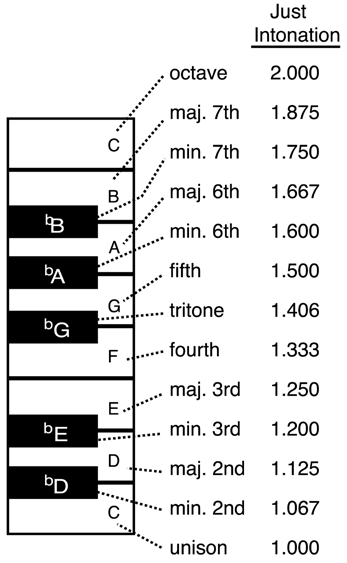
Just intonation is any system of tuning in which all intervals are represented by ratios of small whole numbers. The mathematically simple intervals of just intonation result in clear and consonant sounds. However, just intonation is not very useful in practice because most instruments tuned in it would have to be retuned to change keys. Most contemporary music and musical instruments are based on a different system – that of equal temperament.

 

The mathematics of just intonation and equal temperament

All intervals (pitch relationships) can be stated in terms of the relative frequencies of the individual pitches. For example, if one instrument plays a pitch of 770 cycles per second and another a pitch of 392 cycles per second, the ratio of the two pitches is 770/392, = 55/28, which is a fairly dissonant interval that sounds like a large major seventh. On the other hand, if same two instruments play tones of 800 and 400 cycles per second, respectively, the ratio of the pitches is 2/1, or one octave, which is highly consonant. All intervals, from the octave to the most dissonant, may be defined by such fractional relationships. Generally, the simpler the ratio, the more consonant is the sound. In just intonation, the perfect fifth is 3/2 (1.5), the perfect fourth is 4/3 (1.33), the major third is 5/4 (1.25), the minor third is 6/5 (1.2), and so on.

 

Just intonation is not the system used to tune instruments in current Western culture. These small-number-ratio intervals do not exist on the piano or other Western fixed-pitch instruments, nor in hardly any Western music of the last couple centuries. In the current Western tuning system of 12-tone equal temperament, the octave is divided into twelve equal intervals which must be at least slightly out of tune in order to accomplish the desired equality.

 

The reason that equality necessitates "out of tuneness" may be understood by further examination of the multiplicative, not additive, nature of pitch relationships. As music theory is commonly taught, one adds and subtracts pitches to and from one another: i.e. a major third plus a minor third equals a perfect fifth. This language of common music theory obscures the actual multiplicative relationships of intervals by having the musician add exponential values without necessarily understanding that one is even dealing with exponents. In 12-tone equal temperament, the smallest interval (minor second) must be of a size that will produce an octave (2/1) when multiplied by itself 12 times. The equal-tempered minor second is the twelfth root of 2 or 2^1/12, the major second equals 2^1/6, the minor third equals 2^1/4, the major third equals 2^1/3, etc. The musician who thinks an equal-tempered major third plus a minor third equals a perfect fifth is actually expressing: 2^1/3 × 2^1/4 = 2^1/3+1/4 = 2^7/12.

 

In just intonation, on the other hand, the math is much simpler. One multiplies a major third by a minor third to obtain a perfect fifth: 5/4 × 6/5 = 3/2 (perfect fifth). One divides a perfect fourth by a major third to obtain a minor second: 4/3 × 5/4 = 16/15. Compared to 3/2 and 16/15, 2^7/12 and 2^1/12 sound unfocused.