book-stacking problem
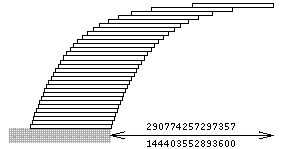
How much of an overhang can be achieved by stacking books on a table? Assume
each book is one unit long. To balance one book on a table, the center of
gravity of the book must be somewhere over the table; to achieve the maximum
overhang, the center of gravity should be just over the table's edge. The
maximum overhang with one book is obviously 1/2 unit. For two books, the
center of gravity of the first should be directly over the edge of the second,
and the center of gravity of the stack of two books should be directly above
the edge of the table. The center of gravity of the stack of two books is
at the midpoint of the books' overlap, or (1 + 1/2)/2, which is 3/4 unit
from the far end of the top book. It turns out that the overhangs are related
to the harmonic numbers Hn, (see harmonic
sequence) which are defined as 1 + 1/2 + 1/3 + ... + 1/n: the
maximum overhang possible for n books is Hn/2.
With four books, the overhang (1 + 1/2 + 1/3 + 1/4)/2 exceeds 1, so that
no part of the top book is directly over the table. With 31 books, the overhang
is 2.0136 book lengths.
Related category
• GAMES
AND PUZZLES
Also on this site:
Encyclopedia
of Alternative Energy & Sustainable Living
Encyclopedia
of History
BACK TO TOP
|
