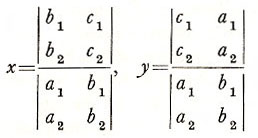A determinant is a mathematical object that is useful in the analysis and solution of systems of linear equations. The determinant of a square matrix, which may represent a set of linear equations, is a number that reveals important properties of the matrix. For example, if the matrix represents a two-dimensional transformation, its determinant gives the ratio by which areas have been changed.

 

A determinant is a square array of numbers, each a member of a field F, used to represent another number in F. Consider the four numbers a₁, a₂, b₁, a₂. The determinant:

 

 

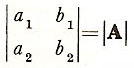
is described as a determinant of order 2 over F and defined to have a value

 

+a₁b₂ – a₂b₁.

 

Notice that transposition (i.e., exchange of rows for columns) does not affect the value of |A|:

 

 

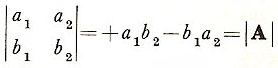
(since multiplication in F is commutative. This is true also of higher order determinants, so that every theorem applied to the columns of a determinant may equally be applied to its rows and vice versa. Notice also that each of the terms in +a₁b₂ – a₂b₁ contains exactly one number from each row and one from each column; thus the value of a determinant of order 2 has 2 terms, one of order 3 has 6 terms, and one of order n has n! terms (see factorial.

 

Other properties of determinants include:

 

· If the elements of any row are multiplied by a factor c, then the new determinant has a value c times that of the original.
·Interchanging two rows of a determinant creates a new determinant with a value equal to that of the original multiplied by (–1).
·If two rows of a determinant are proportional the determinant has a value 0 (a special case of this is when two rows are identical).
·Addition of the elements of one row to the elements of another does not alter the value of the determinant.

 

The theory of determinants closely parallels that of linear simultaneous equations. Consider

 

a₁x + b₁y + c₁ = 0,
a₂x + b₂y + c₂ = 0.

 

These imply that

 

a₂(a₁x + b₁y + c₁) – a₁(a₂x + b₂y + c₂) = 0,
b₂(a₁x + b₁y + c₁) – b₁(a₂x + b₂y + c₂) = 0.

 

These may be restated, respectively, as

 

(a₁b₂ – a₂b₁)y – (c₁a₂ – c₂a₁) = 0
(a₁b₂ – a₂b₁)x – (c₂b₁ – c₁b₂) = 0

 

The solutions, assuming that

 

 

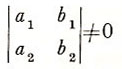
may therefore be expressed in the form