interference

Interference of water waves from two circular sources.
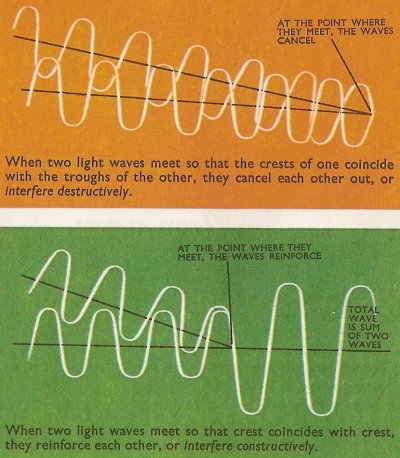
Interference of light waves.
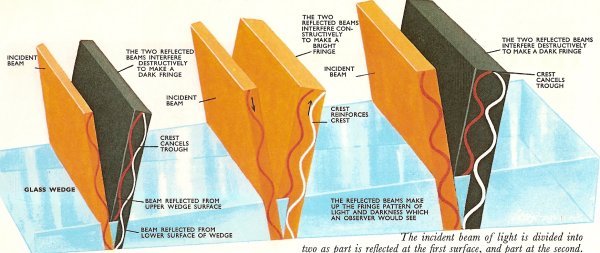
Production of interference fringes.
Interference is the alternate reinforcement and cancellation of two or more wave motions, such as when two beams of light from the same source interact. If the waves in the two beams go up and come down together, they reinforce each other, and the intensity of a combined light beam is increased. The two beams are said to be in phase. But if the two light beams are mixed so that the "ups" of one coincide with the "downs" of the other (i.e., they are out of phase), the ups and downs will cancel out, and darkness results. When waves reinforce, it is called constructive interference, and when they cancel out, it is called destructive interference.
Interference of water waves
Interference of light is difficult to observe since the waves are so small and the vibrations so rapid. However, interference takes place with any kind of wave motion, and the effects of interference can be more easily seen by the examining the behavior of water waves, which are in many ways similar to light waves, but travel more slowly and are more easily noticeable.
 |
Water waves spread out from a disturbance in the center of a pond as light waves spread out from a light bulb. If there are two disturbances in the same pond, waves from one interfere with waves from another. Where the crests of one meet the troughs of another, the waves disappear. They disappear completely if the two disturbances are of equal intensity (i.e., the vibrations of one are the same size as the vibrations of the other), and they stay in the same place if the waves (i.e., of both disturbances) both have the same wavelength (the distance between one crest and the next).
Interference of light
Both these conditions have to be satisfied if two light beams are to add to produce darkness. The two sources of light must both give beams of equal intensity, and both must produce light of the same wavelength. That is, they must be monochromatic.
But although the light from two monochromatic light bulbs will undoubtedly interfere, constructively in some places and destructively in others, this effect will never be visible. The reason for this is that any light source never makes a continuous wave of light. It emits waves in short broken pulses of waves, and no two sources of light will break one pulse and start a new one at the same instant. So even of the ups and downs of the two light beams coincide over one of their short pulses the next pulses will be out of phase, for they will start at different instants and the ups and downs will not coincide. There are so many pulses emitted each second that the alterations in light intensity are too quick to be seen.
Both beams of light must originate from the same source, so that the two sets of pulses start and stop at the same time. They are called coherent. If one of the beams travels a slightly greater distance than the other to the point where they meet, its ups lag slightly behind the ups of the other beam (i.e. get more and more out of phase). When they lag sufficiently for the first wave to have already reached its down when the second is just starting its up, they will obviously interfere destructively.
So the problem of producing visible interference effects is one of dividing a beam of light into two, letting one beam travel slightly farther than the other, and then recombining them. One of the most practicable methods of doing this is to reflect a beam of light onto a very thin wedge of glass. Some of the light is reflected by the first glass surface the beam meets, and the rest travels through the glass, is reflected at the second surface of the wedge and back out of the glass again. In this method there is the added complication that when the light beam is reflected at the second surface, within the glass, it automatically changes its phase so that ups striking the surface are reflected as downs. This second light beam has traveled an extra distance through the glass, so its waves lag slightly behind the waves reflected at the first glass surface. If this extra distance is a half wavelength of the light or 1½, 2½, 3½ ... and so on, wavelengths (the extra half is the result of the change of phase on reflection at the second surface), the light beams interfere constructively. If the extra difference is a whole wavelength or multiples of a whole the beams interfere destructively. Points where the extra distance is the same will be points where the wedge has the same thickness. The wedge appears to have narrow stripes on it, where the light reflected from the glass (this is of course what we see when we look at the glass) has interfered destructively and constructively. The stripes are called interference fringes. They are usually too close together to be seen with the unaided eye, so they must be observed through a microscope.
If the wedge is illuminated with monochromatic or one-color light (a good source of yellow light is common salt burning in a Bunsen flame) the fringes appear as sharp colored and black stripes. However if ordinary white light is used, the fringes are white fringed with the colors of the spectrum, and very few of them can be seen. This is because white light is a mixture of light of different colors (i.e. wavelengths). Since the places on the wedge where the light interferes constructively or destructively depend on the wavelength, the light of different wavelengths in the white light will form dark or colored areas at different places.
Interference fringes can be made a measurable distance apart. Since this distance depends directly on the wavelength of light used, measurement (with a low-power microscope) of the distance between light and dark lines serves as a means of measuring the wavelength of light.


