logic and the tools of philosophy
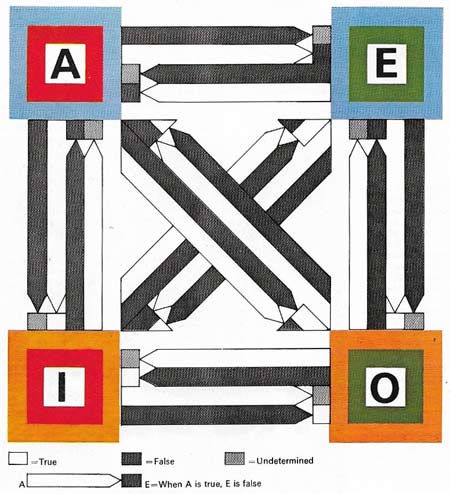
Figure 1. In Aristotelian logic, propositions containing two terms are classified into four kinds (A, E, I, and O) and displayed in a Square of Opposition. Propositions labeled are universal and affirmative (All men are brave); E are universal and negative (No men are brave); I are particular and affirmative (Some, meaning one at least, men are brave); O are particular and negative (Some men are not brave). Specific relationships of truth and falsehood follow from the positions in the square of statements referring to the same two entities. Thus, if proposition A (All men are brave) is false, then its contradictory, O (Some men are not brave), must be true; while A's contrary, E (No men are brave), could be either true or false and is undetermined.
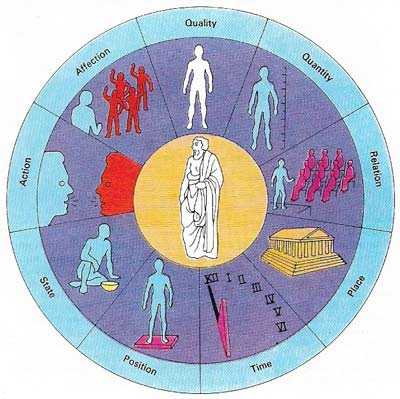
Figure 2. "Category" is a key word in philosophy. Aristotle introduced it first, as a label for ten items he took to be fundamental and irreducible in human discourse. These items are, first, substance (what any statement is about) and next, the nine kinds of statement that can be made about it. For example, Socrates, the central substance in the diagram, can be discussed in terms of quality (he is wise), quantity (he is tall), relations (he is the teacher of his students), place (in the Agora), time (at midday), position (he is standing up), state (he is poor),action (he is arguing), and lastly, affection (he is being abused by some of the students). The study of language was an important philosophical pursuit for Aristotle and his attempt to define its component parts in this way has been followed by many other logicians concerned with the nature and relationships of substances.
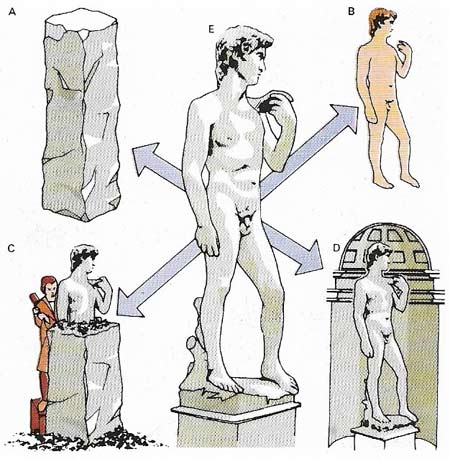
Figure 3. A doctrine of Four Causes was proposed by Aristotle as a means of framing fundamental questions about material and form, means and end. He labeled these four Material, Formal, Efficient and Final. Of a statue (E), for example, the Material cause is stone (A), its Formal pattern is that of a man (B), its Efficient cause is a sculptor (C) and its Final end is as part of a decorative frieze (D). In Aristotle's terminology, the Final Cause is not necessarily someone's conscious intention. The Final Cause of a fetus, for instance, is to achieve its intrinsic end by developing into an adult organism.
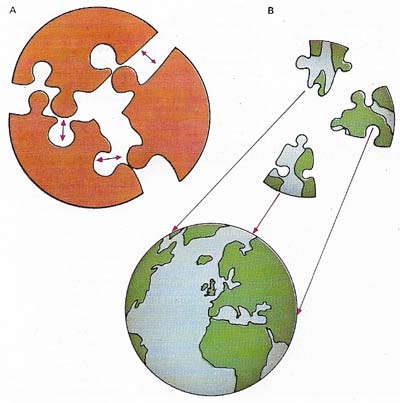
Figure 4. A necessary condition of knowledge is that the statement expressing it be true. There are a variety of theories concerning the ways that the truth of a statement can be verified, of which coherence and correspondence are two. In the coherence theory (A) statements are judged to be true if they form a coherent system in conjunction with other propositions – like the pieces of a jigsaw which one knows to be "right" because they interlock to form a whole, Inn the correspondence theory, (B), a proposition is judged to be true only if there is a fact such as the proposition asserts. Hence the meaning of truth is correspondence with fact that each part of the jigsaw matches part of the known whole.
Figure 5. The mind was seen by empirical philosophers such as John Locke (1632–1704) as rather like an empty box (A) "void of all characters, without any ideas". According to this view, human knowledge has to be derived from whatever experience comes flowing in, and the box develops an internal structure only gradually. Against this picture of open-mindedness, the German philosopher Immanuel Kant (1724 –1804) believed that the mind brings a prior system of categories to organize and interpret data from the senses. Kant's box (B) therefore has its own structure, imposing order on the intrinsically unknown or disorderly materials of experience (although influenced by it).
Logic as a discipline was invented by Aristotle. No doubt people had been reasoning in consistent and logical ways long before Aristotle; but he seems to have been the first to attempt to spell out and formalize the rules of valid inferences (Figure 1).
 |
| Aristotle (384–322 BC), one of the greatest philosophers, founded logic as an academic discipline. For a time, he tutored the boy who was soon to conquer the known world, Alexander the Great. Aristotle directed the first program of research in comparative political science. He both systematized and advanced biological studies. He founded and led the Lyceum the second university) after withdrawing from the first – Plato's Academy. The Middle Ages spoke of Aristotle as "the master of those that know". So in the 1500s and 1600s his name became for all the pathfinders of the new science the epitome of traditional conservative thinking. |
Logic is concerned less with truth or falsity as such than with the transmission of truth or falsity from one set of statements (the premises) to another (the conclusion). Its central concepts are those of logical consequence and of valid inference. If some statement q is a logical consequence of a statement p, then if p is true, so is q; if q is false, so is p. An inference is valid if the conclusion is a logical consequence of the premises from which it was inferred.
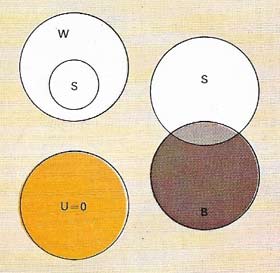 |
| Venn diagrams are devices for the visual representation of logical relations. If all swans (S) are white (W) and not all white things are swans, the S circle must be wholly within the W circle. If some swans (S) are black (B) and not all black things are swans, the S circle must overlap the B. If all unicorns [U] are one-horned (0) and all one-horned creatures are unicorns, then the U and 0 circles must coincide exactly. |
Invalid inferences
In the classical form of the syllogism, with two premises and a conclusion, one example of an invalid inference is known as "the fallacy of undistributed middle": All cows are animals, all herbivores are animals; therefore all cows are herbivores. Here the premises are true, and so is the conclusion, but only accidentally, not by logical necessity. That the inference is invalid can be shown by choosing replacements for each of the descriptive terms in the argument in such a way that although the premises remain true, the conclusion is false. Thus the same reasoning from the true premises: All men are mortal, all gorillas are mortal; would give the false conclusion: All men are gorillas.
Some famous proofs in the early development of mathematics were reductio ad absurdum proofs, a proposition proved by showing that its denial, combined with other true propositions, would lead to an absurd conclusion.
In the 19th and 20th centuries there were many important new developments in mathematical logic.
Aristotelian logic could handle only very limited kinds of deductive reasoning. For instance, Euclidean geometry had long been regarded as a superb example of deductive reasoning; yet Aristotelian logic could say almost nothing about the validity or otherwise of Euclid's inferences.
Kant had endowed mathematical knowledge with a special status essentially different from that of both physics and of logic. Since Kant's view implied that no alternative to Euclidean geometry was conceivable, it became untenable when non-Euclidean geometries were developed. John Stuart Mill (1806–1873) tried the alternative of interpreting mathematics as a part of empirical science; but there were overwhelming objections to this interpretation. A remaining alternative was to interpret it as a branch of logic. It was Gottlob Frege (1848–1925) who first undertook the task of showing that all pure mathematics is deducible from premises that contain only logical terms and are logically true. (This program is known as logicism.) Just as he seemed to have succeeded, Bertrand Russell discovered that the logical foundations of mathematics itself contained fundamental paradoxes.
 |
| Bertrand Russell (1872–1970) was joint author with A. N. Whitehead (1861–1947) of Principia Mathematica. Their main philosophical alto was to show that mathematics was ultimately reducible to logic. That is, every true mathematical statement could be shown to be deducible from premises containing only logical concepts and which are logically true. Their logical system dissolved the traditional Aristotelian distinction between subject and predicate. Russell's theory of descriptions translates the subject-predicate sentence "The King of France is bald" into one that is no longer of the subject-predicate form: "There is an x such that x is King of France and for all y, if y is King of France then y is x; x is also bald." |
Paradox and truth
Logic requires an adequate concept of truth (Figure 4) since it deals with the transmission of truth. But the traditional theory of truth was also beset by paradoxes. One of these, the Liar, had been known in antiquity. The statement: "This statement is false"; if true, is false, and if false, is true. A similar paradox arises as follows. Some adjectives (for example "polysyllabic" and "short") possess the property they denote. These are called "homological". Others (for example, "monosyllabic" and "long") do not. These are called "heterological". Is the adjective "heterological" itself heterological? If it is, then it is not; if it is not, then it is.
Alfred Tarski (1902–1983) eliminated such paradoxes with his semantic theory of truth, which involved a sharp separation between an object-language (the language spoken about) and a meta-language (the language in which the object-language is spoken about).
But when such difficulties can be found in the formulae of mathematics and the language of logic, the problems of establishing a coherent system of thought and then using it to establish scientific truths become obvious. For argument from experience is very different from valid inference, in which the truth of a conclusion can be proved to be logically necessary because denial would involve a contradiction. David Hume (1711–1776) pointed out that since the conclusion of a valid inference can contain no information not found in the premises, there can be no valid inference from observed to unobserved instances. Thus we cannot logically infer that all A's are B, or even that the next A will be B, from the premise that we have observed billions of instances of A's that are B and no instance of an A that is not B. Thus all the laws of science, and nearly all common-sense beliefs, are logically unjustified, this is known as the problem of induction.
Testing scientific hypotheses
One attempted solution, associated with Karl Popper (1902–1994) is to abandon any sort of justifying inference from evidence and to ask of scientific hypotheses that they be subjected to searching attempts to falsify predictions derived from them. If such attempts are successful, the hypothesis has to be rejected. If the hypothesis withstands testing we may not conclude that it is true (the fallacy of affirming the consequent) but we may retain it until we hit upon a less falsifiable one.


