mapping
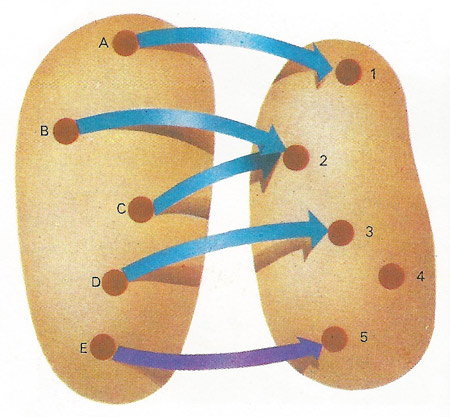
A mathematical map relates one set of objects (e.g., A, B, C, D) to an 'image' set (e.g., 1, 2, 3, 4), symbolized by the arrows. One-to-one correspondence is not necessary; both B and C are sent to 2, D is sent to 3, and nothing is sent to 4. But the map must act on every object in its domain. Without the purple arrow E would be unimaged and the mapping therefore improper.

Light is transmitted by a fiber from one point to another; the bundle maps an object onto its image [A]; it may be deformed by its reduction.
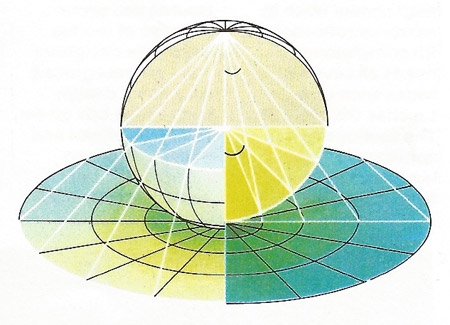
Each point on the globe is sent to one on the map in this diagram. The zenithal projection is mapping the Southern Hemisphere; each point is projected along a line from the North Pole onto a plane touching the South Pole. The equator becomes a circle, as do other lines of latitude. Lines of longitude become radii. The scale is not constant; it increases dramatically towards the edge of the map.
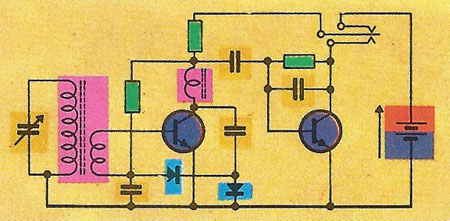
An electronic circuit diagram is a map unconcerned with scale or shape. It shows the connections between the components using stylistic conventions – wires, for example, become straight-line segments.
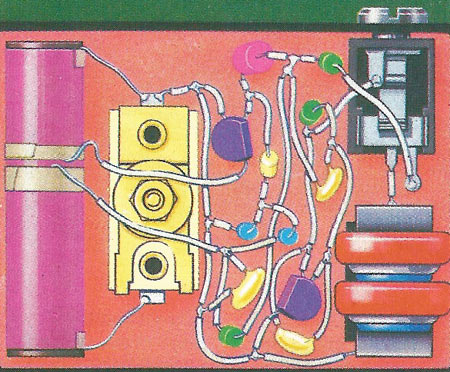
A reflex AM radio-receiver has the circuit diagram shown in the illustration above this one. They don't look alike but are related by a mapping that ensures that the connections to each component are the same in both the physical and schematic layouts. The manufacturer is unconstrained by circuit-diagram conventions and routes the wiring for tight packing of components, for example. But adjacent components may interact, by their electric or magnetic fields, through space.
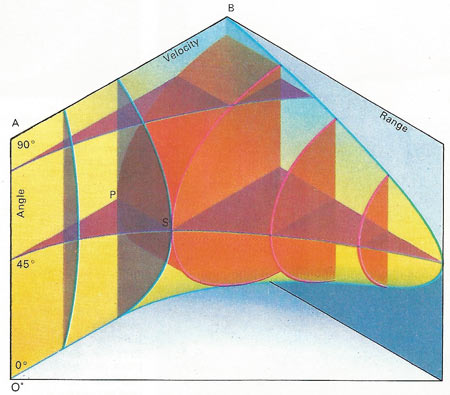
The muzzle velocity and elevation angle of a gun are mapped onto the range of the shell. The plane OAB is a map of angle and velocity; the height of a point (P) represents elevation angle and its horizontal distance from OA represents muzzle velocity. The perpendicular distance PS from the surface at P represents the range for those settings. The surface contour shows that range increases with velocity and is greatest at 45° elevation.

A draftsman's projection is a mathematical map in which many points on the object go to the same point on the image. In the blue triangular projection all the points on the line AB are sent to the top vertex of the triangle. They retain their identity in the yellow square projection, but lose it in the circular red one. All projections "compress" information in this way, so drafting makes use of several.

A weight suspended by a spring [A] and an electrical circuit [B] are mathematical maps of each other. If disturbed, the weight will vibrate with decreasing vigor and an electrical pulse will cause oscillations in the circuit to fade away gradually. Both examples have an energy-storing element (the spring or capacitor), an inertial element (the weight or inductor) and an energy-dissipating element (the water or resistor).
In mathematics, mapping is the assignment to each element a in a set A of at least one element b in a set B, according to a rule f. This is written f: A → B. In a single valued or one-to-one mapping each element a is assigned a single, unique element b. In many cases, the term mapping is considered synonymous with function, but not always (see top diagram).
Math and mapping
The idea of a map is simple: it is any way of relating one set of objects to another set. In a geographical map, every one of the infinite number of points on Earth's surface corresponds (or is "sent" to) just one of the infinite number on the map. Similarly blueprints and circuit diagrams map certain features of a physical object onto a pattern on paper.
Maps and their meaning
One interesting thing about such maps is what they can and cannot do. It is impossible, for example, to map the whole globe onto flat paper without sacrificing some features to preserve others. True directions on a map are impossible to achieve without some distortions. But even distorted mapping is still mathematically acceptable – like the hidden forms found in anamorphic art.
Mathematical maps embrace much more than these simple correspondences of points in space. They deal with anything: points, numbers, sets, and abstract entities with no meaning beyond themselves. They even handle the mapping of a set of objects onto itself. This seeming paradox is commonplace, for example, in secret coding. A code is a rule for replacing each letter of a message by another from the same alphabet; it is a complex mapping of the alphabet onto itself. Similarly, the two-times table relates a number to its double and (if we include fractions in it too) is a mapping of the set of all real numbers onto itself.
One-to-one maps are not the only kind. The "zero-times table" that takes all numbers to zero is a good mathematical map. But the mapping must specify a definite image for every element in its "domain" of operation. Therefore there is the old puzzle of the village whose barber shaves everyone who does not shave himself. This purports to describe a mapping that sends all the shavers to themselves and the non-shavers to the barber. It is not a well-formed mapping because it leaves the barber himself in a paradoxical position. Does he map to himself? (that is, does he shave himself?) If so, he shouldn't, and if not, he should.
By contrast the marriage map between n men and n women (where n is any whole number) is a proper map and defines a possible set of marriages. Assuming that each individual has some order of preferences for his or her n possible partners, then it is a wry outcome of mapping theory that of all possible such maps – ways of pairing off the men and women – one and one only is stable. In all others cases will inevitably occur in which a couple, not married to each other, will prefer each other to their own spouses.
Maps between one thing and another
The above mappings are examples of discrete instead of continuous maps. Unlike those of points on a surface or a set of all real numbers they handle a finite set of elements only. The mapping of telephone subscribers onto their telephone numbers is like this too. Each subscriber has his own number, but not all numbers are represented. For example there is no number 000 0000. A reservoir of possible but unused numbers is held by telephone companies. This map illustrates a new point too. Our previous examples sent points to points, numbers to numbers, people to people; this one sends people to numbers.
The mapping of one set of entities onto another apparently quite different set is a powerful mathematical technique. For instance, analytical geometry maps geometry onto algebra. Each geometrical curve or line is sent to its corresponding equation; and for each geometrical theorem there is a corresponding identity. The mapping preserves the relational features of geometry so that geometrical problems of great difficulty (for example, those in many dimensions) can be mapped by easier-to-handle algebra, solved and then mapped back to give the required geometrical truth.
Morse code is another example of such mapping. Letters and numbers are mapped onto combinations of dots and dashes. These in turn can be transmitted as short and long flashes of light or pulses of electric current. At the receiving end the dots and dashes are mapped back to letters and numbers.
A vast range of scientific and technical enterprise depends on mapping from the real world into symbolic systems that preserve the important features. An astronomer maps the positions of the heavenly bodies into terms of a set of equations. From the ensuing calculations, he can recover terms that map back into future positions of the bodies and perhaps predict an eclipse.
Mapping: theory into practise
It is the business of mathematical science to make sure that mappings work. All scientific theories are maps in the sense and so are the calculations and designs of an engineer who decides on paper that an aircraft as yet unbuilt can fly. Like geographical maps of the globe, these maps sacrifice some features to preserve others and so they are incomplete. They fail totally in some areas of experience and distort so badly in others that they are useless for any practical purposes.


