number patterns
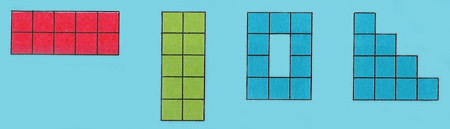
Figure 1. Some possible shapes made from 10 squares. The fourth shape shows that 10 is a triangular number.
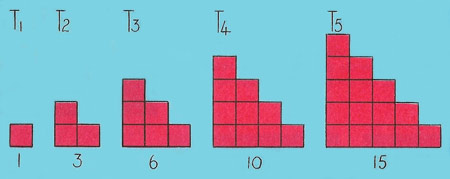
Figure 2. The first five triangular numbers.
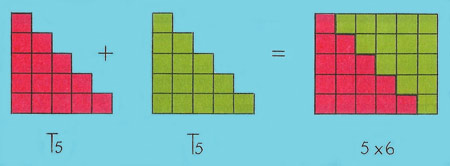
Figure 3. The sum of T5 and T5.
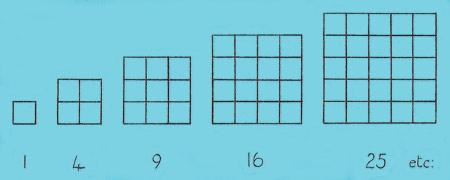
Figure 4. Square numbers 1 to 25.
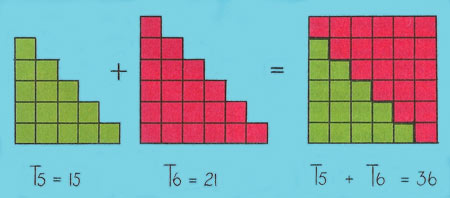
Figure 5. Adding T5 and T6 gives a square number (36).
Could you find the sum of the numbers from 1 to 100 very quickly? Try to do so before reading any further.
We are going to see how an appreciation of the pattern of numbers would help to solve a problem of this type.
Triangular numbers
If you were given 10 small squares you could arrange them into various patterns, some of which are illustrated in Figure 1. The fourth pattern is triangular shaped, and any number which has the property of being represented by a triangular pattern is called a triangular number. We call the first triangular number T1, the second T2, and so on. We call 1 a triangular number because it is the basis of the triangular numbers. Fig 2 shows the first five triangular numbers.
We notice that T1 = 1, T2 = 1 + 2, T3 = 1 + 2 + 3, T4 = 1 + 2 + 3 + 4,...
Remember that our original problem was to find T100. Now if we take two of our T5 shapes, they can be arranged to form a rectangle, as shown in Figure 3.
Two T5's = 5 × 6,
So T5 = (5 × 6)/2
Similarly, T6 = (6 × 7)/2.
Consequently, T100 = (100 × 101)/2 = 50 × 101 = 5050
and here is the answer to our original problem.
No try to find the sum of the numbers from 1 to 1000.
It is interesting to note that any number can be expressed as the sum of three or fewer triangular numbers. For instance, 14 = 10 + 3 + 1, 12 = 10 + 1 + 1, 30 = 21 + 3 + 6.
Square numbers
The numbers shown in Figure 4 have a related square form and they are consequently called square numbers. This is also why a statement such as 16 = 42 is read as "sixteen equals four squared". For a similar reason, 27 = 33 is read as "twenty-seven equals three cubed".
Now let's try adding sequences of odd numbers:
1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 = 5 + 7 = 16
1 + 3 + 5 + 7 + 9 = 25
The answer is always a square number, and Fig 6 below explains why.
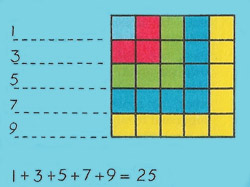 |
| Fig 6. 1 + 3 + 5 + 7 + 9 = 25
|
Check on some further sequences.
Triangular numbers and square numbers
Here are the first few triangular numbers again: T1 = 1, T2 = 3, T3 = 6, T4 = 10, T5 = 15, T6 = 21.
There is a simple connection between the triangular numbers and square numbers. That is, the sum of successive triangular numbers is a square number.
1 + 3 = 4
3 + 6 = 9
6 + 10 = 16
and so on
Figure 7 explains why.
multiplication tables
The multiplication tables, as well as the individual numbers, have their own associated geometrical shape.
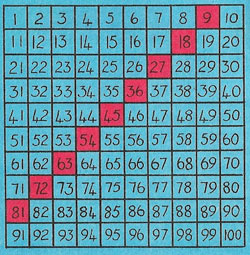 |
| Fig 7. The multiplication table with multiples of 9 highlighted.
|
In this diagram the multiples of nine have been shaded in, resulting in a straight-line pattern. What can be noticed about these numbers: 9, 18, 27, 36, 45, and so on?
The sum of the digits in each number is a multiple of 9.
The 10's digits increase 1 at a time and always 1 less than the multiplier.
The units digits decrease 1 at a time.
Could you formulate a rule for multiplying nines by an digit?
There are many number patterns involving the number nine, e.g.:
1 × 9 + 2 = 11
12 × 9 + 3 = 111
123 × 9 + 4 = 1111, etc.
9 × 9 + 7 = 88
98 × 9 + 6 = 888
987 × 9 + 5 = 8888 etc.
Try to explain why these number patterns occur. Construct the other multiplication table patterns on squares marked 1 to 100 and see what other number properties you can discover.


