parallel lines
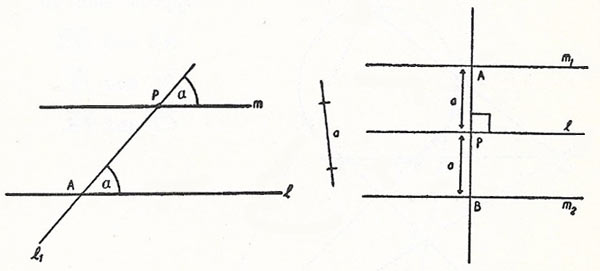
Figure 1. Parallels to a line.
Parallel lines are two or more lines that lie in the same plane and never intersect each other. They are equidistant from each other and have the same slope.
1. To construct a straight line m through a given point, parallel to a straight line I. Draw through the given point P an arbitrary straight line l1 intersecting l in the point A. I and l1, form together the angle α (Figure 1 left). At P on l1 lay out the angle α, on the same side of A, and in the same sense, from AP. Then the free arm of the new angle gives the direction of the required parallel m. l1 may conveniently be chosen to be perpendicular to m (α = 90°).
2. To construct a straight line m parallel to a given straight line I and at a distance a from it (Figure 1 right). Take a point P on I and erect the perpendicular to I at this point. Describe a circle with radius a about P. This intersects the perpendicular in two points A and B, such that P lies between A and B. Draw the lines parallel to I through A and B. There are two lines, m1 and m2 with the required property.


