perpendicular
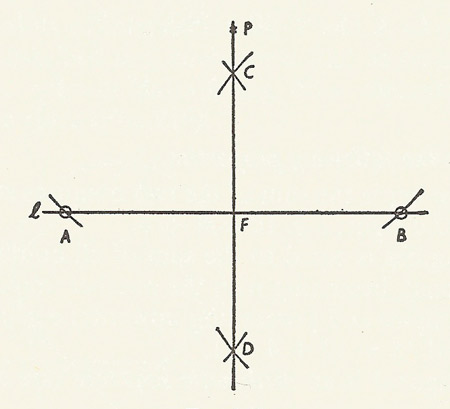
Construction of a perpendicular.
To be perpendicular is to be at right angles. Two lines, planes, etc., are said to be perpendicular if they are 90° apart.
Perpendicular bisector
The perpendicular bisector of a given line segment AB is the straight line perpendicular to AB, and passing through its mid-point. The perpendicular bisector of a segment is the axis of symmetry of the segment. The perpendicular bisectors of the three sides of a triangle intersect in the center of the circumcircle.
Construction of a perpendicular
To drop a perpendicular onto a straight line.
Construction: Given a straight line l and a point P outside the line. Describe a circle (of arbitrary radius) about P so that it intersects l in two points A and B. About A and B draw circles large enough to intersect and join their points of intersection, C and D. The required perpendicular lies on the line through C and D, and is the join of P to the point F where L and CD intersect.


