A sequence, also called a progression, is an ordered set of numbers (e.g., 2, 4, 6, 8, ...2n, ...), which may be finite or infinite in length. The members of the sequence are linked by a common mathematical formula. Infinite sequences may or may not be convergent (tend to a single limit). The sequence 0, 0.9, 0.99, 0.999, ... for example is convergent, tending to the limit 1. Among the different types of sequence are arithmetic sequences, geometric sequences, and harmonic sequences.

 

A unmilled sequence is a sequence that first increases and then decreases.

 

Point-sequence

If according to some prescribed rule a first point P₁ determines a second P₂, and P₂ determines a third P₃, and so on, these points are said to form a point-sequence:

 

P₁, P₂, P₃, P₄, ...

 

The points dealt with can be either in a plane or in three-dimensional space. Point-sequences are closed later to number-sequences. Thus, if the points are specified by their coordinates, three number sequences are formed from the coordinates P_n (x_n , y_n , z_n) of the general point

 

x₁, x₂, x₃, ..., x_n, ...

y₁, y₂, y₃, ..., y_n, ...

z₁, z₂, z₃, ..., z_n, ...

 

Conversely, given an arbitrary number-sequence a₁, a₂, a₃, ..., a point-sequence can be derived in which the number a_n is associated with the point A_n (a_n , 0) of the plane (x, y).

 

A point-sequence is said to converge to the point A (P_n → A) if the distance P_n A form a null sequence. A point-sequence which is not convergent is said to be divergent. E.g. suppose the following points are given in a plane:

 

 

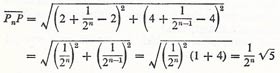The sequence converges to the point P (2, 4), since the sequence of distances

 

 

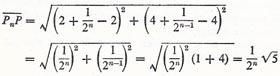is a null sequence.