thermal conductivity, measurement
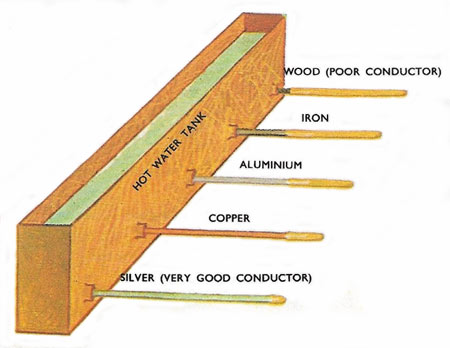
Figure 1. Testing the conductivity of a range of materials.

Figure 2. A large quantity of snow melts down to very little water. This is because snow is over 80% air which makes it a very good thermal insulator.
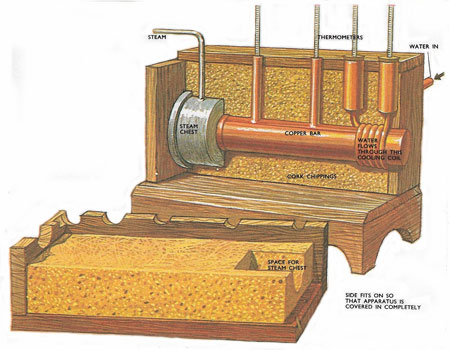
Figure 3. Searle's apparatus for finding the thermal conductivity of good conductors such as copper or aluminum. The character of metals which makes them good conductors of electricity also makes them conduct heat easily.
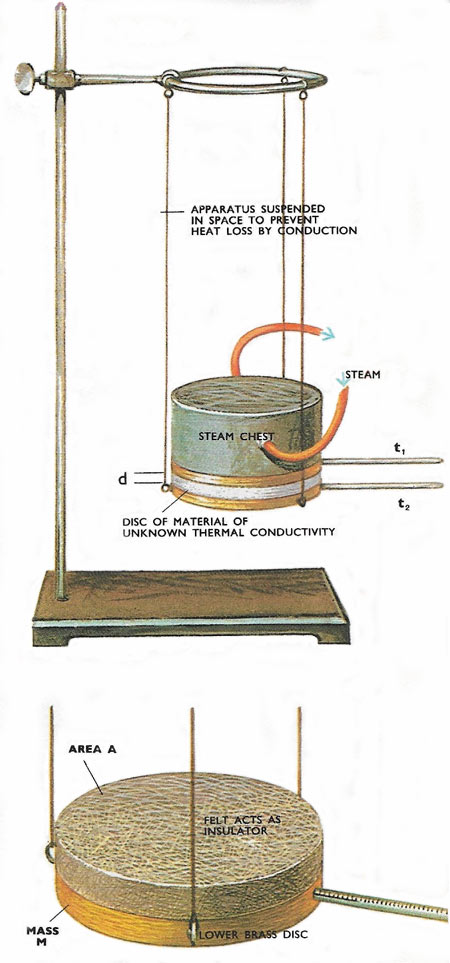
Figure 4. (top) Lees and Chorlton disk. (bottom) The lower brass disk is heated up on its own by putting it in contact with the steam chest. The top side is covered with felt so no heat is lost through the side. The temperature falls and every few minutes it is plotted on a graph.
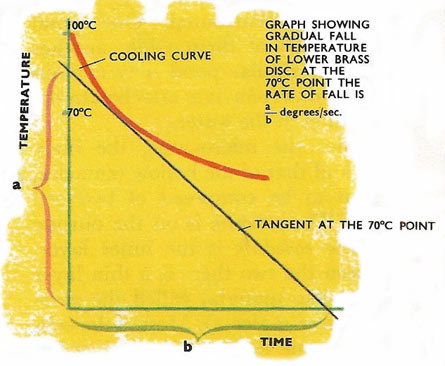
Figure 5. The gradient of the graph at 70°C is the rate of fall of temperature at 70°C. If the mass of the brass plate is M the specific heat of brass S, then MS a/b is the number of calories of heat lost per sec. This is equal to the heat flowing through the disk. If A is the area of the disk of material then heat flowing per second through 1 cm2 = MSa/Ab. This equals thermal conductivity × temperature gradient. The temperature gradient across the disk of material is (t1 – t2)/d so MSa/Ab = thermal conductivity x (t1 – t2)/d.
Some materials feel warm to the touch – others like marble do not. The difference in the materials is their thermal conductivity (Figure 1). Metals have a high thermal conductivity – they conduct heat away from the fingers rapidly, and so feel cold, whereas gases such as air are the lowest in the scale. Materials with a lot of spaces in them such as cotton wool consequently make good insulators, though no material is a perfect insulator (Figure 2).
Heat is energy of motion in the atomic particles of a substance, and heat flow is the diffusion of this energy. Heat passes through a body because there is a temperature gradient between the ends. This measures the steepness of temperature and is another way of saying that one end is hotter than the other. In fact temperature gradient is the difference of temperature between each end, divided by the distance between each end.
As with electrical conduction there is a simple law of heat conduction which can be applied to the heat flowing out through the walls of a room, or the flow of heat along a bar such as the handle of a saucepan.
Heat flow per second through 1 square centimeter = thermal conductivity × temperature gradient.
The experimental way of finding the thermal conductivity of any material consists in measuring the heat flow when the temperature gradient is known. There are two sorts of experiment – those for good conductors and the other for materials of low conductivity, i.e. insulators.
Searle's bar method
The material, usually a metal, is made into a long bar. One end is soldered to a heat source such as a steam tank. A cooling coil through which a known quantity of water is passed per second is wrapped around the other end. Two thermometers along the bar at a known distance apart make good thermal contact with it through mercury cups. A further two thermometers take the temperature of the water as it leaves and enters the coil. In order that no heat loss occurs through the sides of the bar, the bar and coil are surrounded by a box filled with a good insulator such as cork chippings. When steam is let into the tank the heat starts to flow along the bar. After a while some of this heat reaches the coil and the flowing water removes the heat. When steady conditions become established, i.e. all the thermometers stay at a fixed reading, the heat passing along the bar is entirely removed by the water in the coil at the far end (Figure 3).
On measuring the water flow and its rise in temperature, the total heat removed by the water per second is found. Once the temperature gradient is read off the conductivity is known. The temperature gradient is the difference in the other two thermometer readings divided by the distance between them.
The apparatus reaches a steady condition in which all the heat flowing through the disc is lost by convection and radiation from the lower plate. t1 will be at 100°C and t2 at a lower temperature. To find the heat loss of the brass plate at this temperature another experiment must be performed.
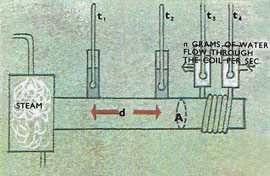 |
n grams of water flow through the cooling coil per second.
Rise in temperature of n grams = t3 – t4
Heat in calories removed by this water = n(t3 – t4).
Heat flow through 1 cm2 = n(t3 – t4)/A
As the bar is insulated, no heat is lost to the side, and the temperature gradient is constant and can be taken between any two points along the bar.
Temperature gradient = (t1 – t2)/d
Heat flow through a cm2/s = thermal conductivity x temperature gradient.
N(t3 – t4)/A = thermal conductivity × (t1 – t2)/d so the thermal conductivity for the material of the bar is discovered.
 |
Method for poor conductors
For materials which are bad conductors of heat, such as flannel, a long bar would conduct hardly any heat so the specimen is made into a flat disk a few millimeters thick and enclosed between two heavy brass plates in contact with thermometers. The upper brass plate makes up the bottom of a steam chest and the whole apparatus is suspended in air by three strings to minimize conduction losses. This apparatus is called the Lees and Chorlton disk (Figure 4). Steam is passed into the chest and eventually the whole system comes to equilibrium with the upper thermometer at 100°C and the lower one at, say, 70°C. All the heat received by the lower plate through the disk is now being lost by convection and radiation to the surroundings. Since the heat lost per second is the same as the heat received through the disk per second, the second part of the experiment consists of finding the rate of cooling of the lower plate at 70°C.
The lower brass disk is heated up to 100°C, one side of it being covered with a good insulator such as felt, because as in the experiment, no heat is lost through this side. Slowly the brass disk starts to cool. Its temperature is read at intervals and plotted on a graph against time. The gradient of this graph at the point 70°C is the rate of cooling of the plate at this point (Figure 5). From this rate of cooling can be found the heat lost in calories per second. This is equal to the rate of flow of heat through the disk. The thermal conductivity multiplied by the temperature gradient is them equal to this heat flow.
These two methods are the usual way of finding the thermal conductivity but other specialised methods are used for liquids and gases.


