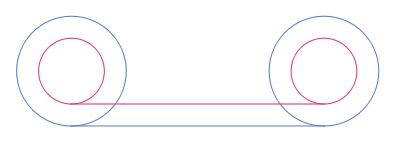
Aristotle's wheel is a paradox mentioned in the ancient Greek text Mechanica, whose author is unknown but is suspected by some to have been Aristotle. The paradox concerns two concentric circles on a wheel, as shown in the diagram. A one-to-one correspondence exists between points on the larger circle and those on the smaller circle. Therefore, the wheel should travel the same distance regardless of whether it is rolled from left to right on the top straight line or on the bottom one. This seems to imply that the two circumferences of the different sized circles are equal, which is impossible. How can this apparent contradiction resolved? The key lies in the (false) assumption that a one-to-one correspondence of points means that two curves must have the same length. In fact, the cardinalities of points in a line segment of any length (or even an infinitely long line or an infinitely large n-dimensional Euclidean space!) are all the same.