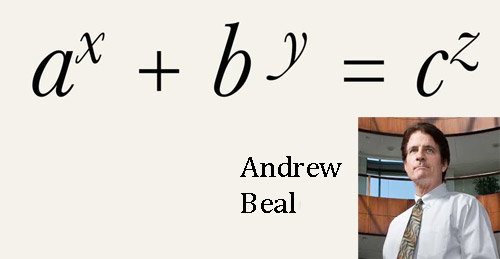
In 1997 the Texan financier Andrew Beal offered $75,000, later increased to $100,000, to the first person who could prove or provide a counterexample to the following conjecture:

If a ^x + b ^y = c ^z, where a, b, c, x, y, and z are all positive integers, and x, y, and z are greater than two, then a, b, and c have a common factor (greater than one). Fermat's last theorem, which was proved in 1994, is a special case of Beal's conjecture. However, no one has yet been able to use this fact to prove or disprove the conjecture, nor has anyone been able to come up with a counterexample as a disproof. It is known that for any set of three exponents x, y, and z, each greater than two, there can be at most finitely many solutions. But is this finite number zero? The prize remains unclaimed.