Benford's law
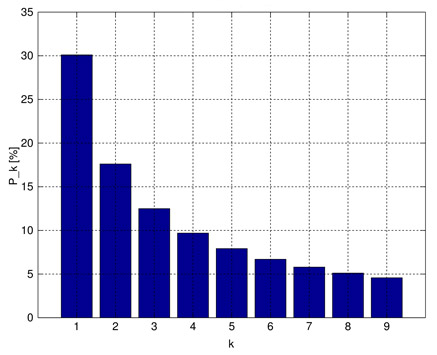
The distribution of first digits, according to Benford's law. Each bar represents a digit, and the height of the bar is the percentage of numbers that start with that digit.
If a number is chosen at random from a large table of data or statistics, such as stock quotations, populations of towns in Germany, or half-lives of radioactive atoms, the chance that the first digit is 1 is about 30.1%, that the first digit is 2 is about 17.6%, that it is 3 is 12.4%, ... , and that it is 9 is 4.5%. These figures fit the rule that the probability that the first digit is d is log10(1 + 1/d). This rule is called Benford's law after the American physicist Frank Benford who publicized his findings in 1938.1 The same discovery had been made 57 years earlier by the astronomer and mathematician Simon Newcomb who noticed that the front pages of logarithm tables tended to be more dog-eared than pages later on.2
Benford tested thousands of different collections of data, including the surface areas of 335 rivers, specific heats and molecular weights of thousands of chemicals, baseball statistics, and the street addresses of the first 342 people listed in the book American Men of Science. All these seemingly unrelated sets of numbers followed the same first-digit probability pattern as the worn pages of logarithm tables suggested. In all cases, the number 1 showed up as the first digit about 30% of the time, more often than any other, and seven times more often than the number 9.
It seems extraordinary. Why shouldn't the numbers 1 to 9 take equal turns to be the first digit? Benford's findings have been verified by other researchers. The larger and more varied the sampling of numbers from different data sets, it has been found, the more closely the distribution of numbers approaches what Benford's law predicted. Moreover these probabilities are scale invariant and base invariant. For example, it doesn't matter whether the numbers are based on the dollar prices of stocks or their prices in yen or marks, nor does it matter if the numbers are in terms of stocks per dollar; provided there are enough numbers in the sample, Benford's law will hold. 3, 4
References
1. Benford, F. "The Law of Anomalous Numbers." Proc. Amer. Phil.
Soc., 78: 551- 572 (1938).
2. Newcomb, S. "Note on the Frequency of the Use of Digits in Natural
Numbers." Amer. J. Math., 4: 39-40, 1881.
3. Hill, T. P. "The First Digit Phenomenon." Amer. Sci., 86:
358-363 (1998).
4. Raimi, R. A. "The Peculiar Distribution of First Digits." Scientific
American, 221: 109-119 (Dec. 1969).


