binary

Figure 1. Binary numbers.
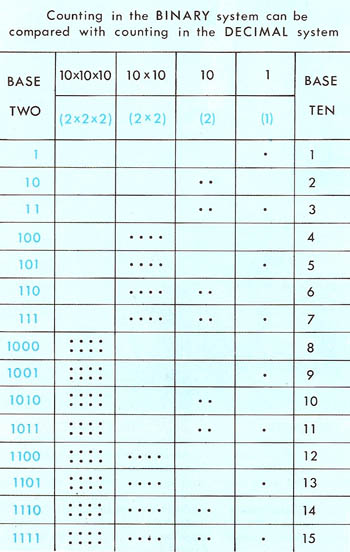
Figure 2. Counting in binary.
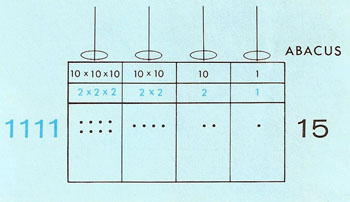
Figure 3. Binary equivalent of 15.
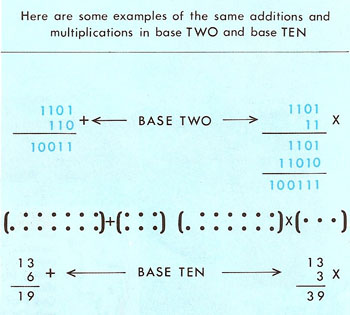
Figure 4. Addition and multiplication in binary.
There are 10 kinds of people in the world, those
who understand binary math, and those who don't.
—anonymous
Binary is the simplest positional number system and the natural one to use when dealing with computers; it employs just two symbols, 0 and 1, which correspond to the possible states of an off-on switch. Binary arithmetic was first investigated by Gottfried Leibniz in 1672, though he didn't publish anything about it until 1701.
Each place to the left in a binary number represents the next highest power of two. The binary number 101102, for example, means 1 × 24 + 0 × 23 + 1 × 22 + 1 × 21 + 0 × 20, or 2210 in the familiar decimal notation. Non-integers can be represented by using negative powers, which are set off from the other digits by means of a radix point (called a decimal point in base 10). The binary number 11.012 thus means 1 × 21 + 1 × 20 + 0 × 2-1 + 1 × 2-2 which equals 3.2510. A number that terminates in decimal doesn't necessarily do so in binary (for example, 0.310 = 0.0100110011001...2), and vice versa. An irrational number, however, is non-periodic in both systems; for example, π = 3.1415926...10 = 11.001001000011111...2.
As the scientist-hero of Fred Hoyle's science fiction novel A For Andromeda explains:
It's arithmetic expressed entirely by the figures 0 and 1, instead of the figures 1 to 10, which we normally use and which we call denary. 0 and 1, you see, could be dot and dash... the binary system is basic; it's based on positive and negative, yes and no ... – it's universal.
Because of its fundamental nature it has been suggested that binary may represent a lingua franca for communication between technological civilizations in the Galaxy.
Working in binary
At first, long numbers in the binary system seem a little difficult to understand (Figure 2). If we look at the diagram below it will make it clearer. Just as in the decimal system, the right-hand column is for units. The next column is for the number of 10s, the next for (10 × 10)s, and the left-hand column for (10 × 10 × 10)s. If we want to change a binary number into a decimal number we must remember that 10 in the binary system is the equivalent of 2 in the decimal system.
Let's change the number 1111 in the binary system into its equivalent in the decimal system (Figure 3). The right-hand number is 1. The next number, the binary equivalent of 10, is 2. The next (10 × 10) equals 2 × 2, or 4. And the left-hand number corresponds to (10 × 10 × 10), so in the decimal system it is 2 × 2 × 2, or 8. Add these together, and we get 15.
When adding in the binary system, it's important to remember that 1 × 1, which would equal 2 in the decimal system, equals 10 in the binary system. When multiplying in the binary system, we write it out as in long multiplication (Figure 4).


