Collatz problem
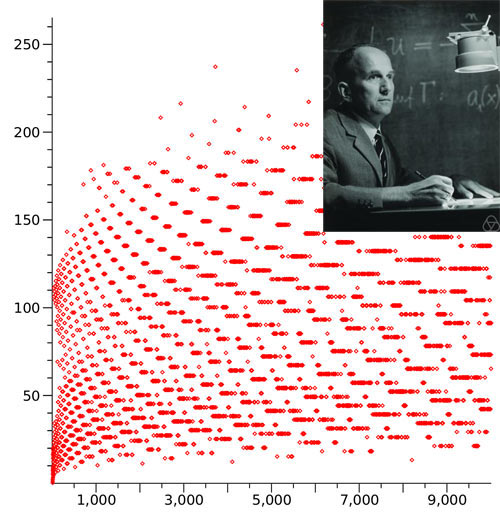
Numbers from 1 to 9999 and their corresponding total stopping time.
In 1937 German mathematician Lothar Collatz (1910–1990) made a surprising discovery. If you start with any whole number, divide it by 2 if its even and triple it and add 1 if it's odd, and keep repeating this process over and over again, you'll eventually end up with the number one. For instance if you start with 20, and give it the Collatz treatment, you get the sequence 20, 10, 5, 16, 8, 4, 2, 1. Start with 17 and the sequence runs 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. Collatz conjectured that arriving at 1 will always be the end point.
Needless to say, mathematicians have tried to find an exception, but so far they've drawn a blank. It's a simple matter to program a computer to keep checking successively bigger numbers until it runs out of time or its owner out of patience. Mathematicians have applied this brute-force approach and shown (at the time of writing) that there are no violations of the hypothesis out to a value of 87 × 260. But this signifies nothing. The next biggest number that hasn't been checked might be the one that breaks the mould: that leads to a sequence that blows up to infinity or gets stuck in an endlessly repeating loop.
The Collatz problem, or Collatz conjecture, is also known variously as the 3n + 1 problem, Kakutani's problem, the Syracuse problem, Thwaites' conjecture, and Ulam's conjecture. The sequences of numbers produced by the Collatz problem are sometimes known as hailstone sequences.
The beauty and mystery of what Collatz suggested is that anyone, even a child as young as eight or nine, can grasp what it's about. It's no exaggeration to say that it's the easiest-to-understand open problem in all of maths, having the appearance almost of a party trick. But the fact that it's remained open since it's discovery in Victorian times is a measure of its true depth. It relates not just to number theory but to issues of decidability, chaos, and the very foundations of mathematics and computation. Paul Erdös said of it: "Mathematics is not yet ready for such problems".
British mathematician Bryan Thwaites (1996) has offered a £1,000 reward for a resolution of the problem. However, John Conway has shown that Collatz-type problems can be formally undecidable, so it not known if a solution is even possible.
Hailstone sequence
A hailstone sequence is a sequence of numbers produced by the rules of the Collatz problem. For n = 5, the sequence is 5, 16, 8, 4, 2, 1, 4, 2, 1, ... For n = 11, the resulting sequence is 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, ... The name "hailstone" comes from the fact that the numbers in these sequences rise and fall like hailstones in a cloud before finally falling to Earth. It seems from experiment that such a sequence will always eventually end in the repeating cycle 4, 2, 1, 4, 2, 1, ..., but some values for n generate many values before the repeating cycle begins. An unsolved mystery is whether all such sequences eventually hit 1 (and then 4, 2, 1, 4, 2, 1, ...) or whether there are some sequences that never settle down to a repeating cycle.
Reference
1. Guy, Richard K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, 1994.

