Coulomb's law for magnets
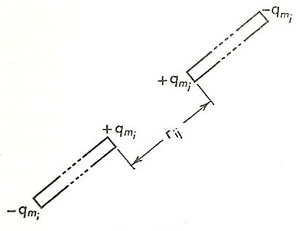
Figure 1. The poles of long thin magnets.
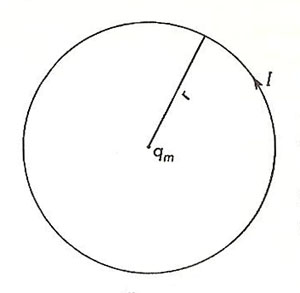
Figure 2. Circular current and magnetic pole.
Coulomb's law for magnets is the analog in magnetism of Coulomb's law for electric charges. Coulomb's law describes the force between magnetic poles.
The conclusion that there were two types of magnetism, analogous to the two types of static electricity, was a natural consequence of the discovery that the poles of a magnet either attract or repel one another. The north (i.e. north-seeking) pole was said to be positive, whereas the south pole was negative.
Attempts were made to separate the positive and negative poles of a magnet by breaking the magnet into two pieces, but it was always found that negative and positive poles, respectively, appeared on the two sides of the break. It was, therefore, reluctantly accepted that the privilege of independent experience, enjoyed by electric charges, is not a prerogative of magnetic poles. Whenever a positive pole is discovered in nature, it is inevitably associated with a negative pole of equal strength. (This fact is explicable on the modern view that the magnetic properties of a magnet are due to the elementary closed currents that it contains.)
The problem of obtaining "free" poles, in order to determine the force between them, was overcome by using long, thin magnets. Here, as shown in Figure 1, the positive pole was sufficiently far removed from its associated negative pole as to be practically isolated from it. The law of force between poles was investigated by Charles Coulomb, using the same torsion balance with which he established the law of force between electric charges, and was found to be similar in form to that for charges. Thus, the magnitude of the force between two poles of strength qmi and qmj, located a distance rij apart, is written as:
F = Cqmiqmj / rij2 (1)
where the value of C, the constant of proportionality, depends upon the system of units employed and the magnetic properties of the intervening medium. The vector form of Coulomb's law for magnets is similar to that for electric charges, in that the force between poles acts along the line joining them.
The equation above is the fundamental equation for magnetostatics. From it a unit pole can be defined. Then, by analogy to electrostatics, the ideas of magnetic field, magnetic potential, and so on, can be developed. The primary entities, in this magnetostatic picture, are small bar magnets possessing positive and negative poles, qm and - qm, which are separated physically from one another. This method of representing elementary magnets, although artificial, is useful for handling many aspects of magnetism. For example, it provides a convenient method of calculating the external effect of a large assembly of elementary closed currents, as in a compass or ordinary magnet. In addition, the small bar magnet is a valid replacement for a single closed current when one is calculating magnetic effects at distances which are large by comparison to the dimensions of the current loop.
Coulomb's law in the mks system of units
By definition, the mks unit pole, when placed at a point in space where the magnetic induction is 1 weber per square meter, experiences a force of 1 newton. Thus, the force experienced by a pole of strength qmj mks units is given by
Fj = Bqmj (2)
where B is the value of the magnetic induction at the position of the pole. By comparing the two equations we have written, we see that the magnitude of the magnetic induction at a distance r from a magnetic pole qm is given by
B = Cqm/r 2 (3)
Let us now deduce the value, for the mks system of units, of the constant C in Coulomb's law for magnetic poles. This we can do by looking at the interaction between a circular current and a magnetic pole located at its center (Figure 2). We shall calculate, and then equate, the force exerted by a current upon the pole and the force exerted by the pole upon the current.
The circular current in a vacuum produces an induction at its center of magnitude
B = μ0I/2r webers/m2 (4)
Hence, the force experienced by the pole qm is
F = Bqm = μ0Iqm/2r newtons (5)
Meanwhile, the pole produces an induction given by equation (3). Since this induction is everywhere normal to the direction of the current, the current experiences a force
F = BIl = (Cqm/r 2)(I)(2πr) newtons (5)
From Newton's third (action and reaction are equal and opposite), these two forces are equal. Equating them, we find
2πCqmI/r = μ0Iqm/2r (6)
or C = μ0/4π (7)
Substituting this value in equation (1), we have Coulomb's law for magnetic poles in the mks system:
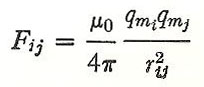
The units of the mks pole are amperes-meters.


