crystal
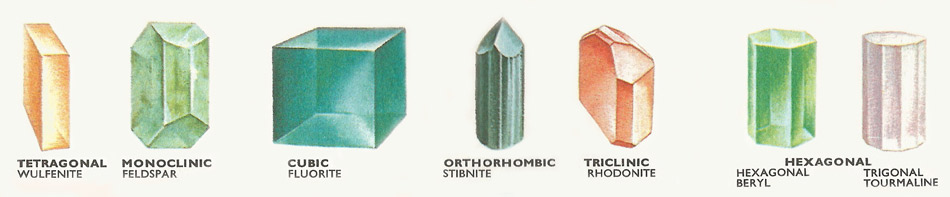
Figure 1. The seven systems of crystals.
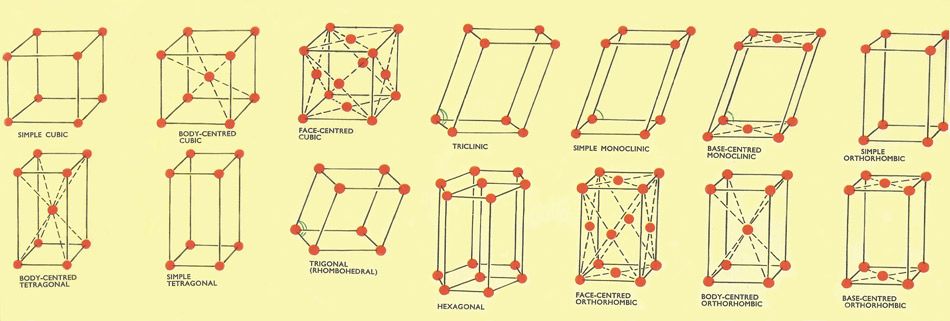
Figure 2. The 14 crystal lattices.

Figure 3. Quartz forms long hexagonal shaped crystals with pointed ends. The line diagram alongside shows the ideal geometrical shape which a perfect crystal would assume.
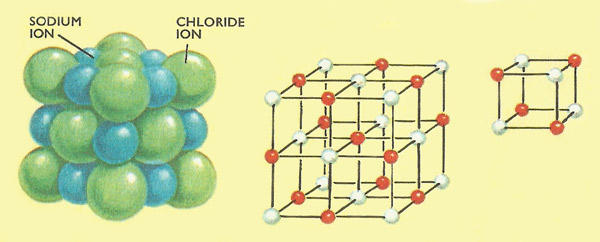
Figure 4. (Left) A small fragment of common salt contains equal numbers of sodium ions and chlorine ions arranged in a regular repeating pattern. (Center) The pattern is shown clearly in this model where red balls represent sodium ions and white balls represent chloride ions. (Right) The basic unit of the repeating or lattice is a simple cube.
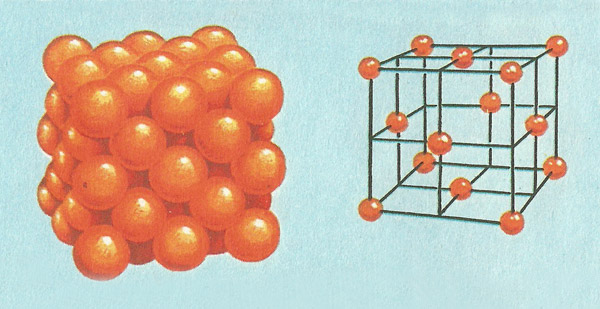
Figure 5. (Left) The arrangement of atoms in a small fragment of copper. (Right) A model of the basic unit is a cube with atoms at each corner and at a center of each face.
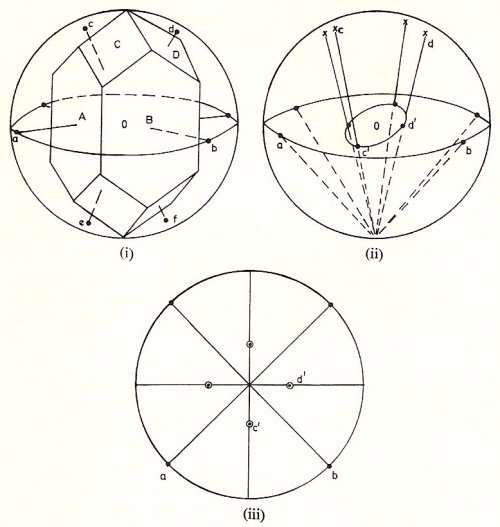
Figure 6. Crystals may be idealized by representing their faces by a system of normals drawn perpendicular to the faces, where the normals a, b, c, d are drawn perpendicular to the faces A, B, C, D, respectively (i). As a further refinement these normals are represented by points such as a, b, c, d at which they intersect the surface of a sphere (ii). The problem then is to study the arrangement of such collections of points since the symmetry of this arrangement represents the symmetry of the crystal. In the example shown, the crystal symmetry comprises a fourfold tetragonal axis, which is vertical. If we had also included points to represent the underneath faces of the crystal, which have been omitted for clarity, we should see that there is also a horizontal plane of symmetry. The fourfold axis and the plane of symmetry are examples of symmetry elements. These elements are such that when they operate on the collection of points then the collection returns to its initial arrangement. Thus the operation represented by a fourfold axis is a rotation through 90° and it will be seen that when this operation is carried out by a vertical axis on the set of points shown in (ii) a set of identical positions is produced. Investigation shows that there can be only a limited number of combinations of symmetry elements grouped together in this way and passing through a point, indicated as O, and it is a purely mathematical problem to work out this total number.
In (ii) each crystal face, or normal direction, is represented by a point such as a, b, c, or d on the surface of a sphere. For each of these points, such as c or d, we draw a line to the south pole of the sphere as shown in (ii). The points, such as c', d' where these lines intersect the equatorial plane of the sphere, are the stereographic representation of the crystal face. Figure (iii) is the stereogram for the crystal shown in (i). Points a, b on the circumference of the circle correspond to faces A, B which are vertical in the original crystal. For the crystal faces which are on the underneath of the crystal we shall have to join the ends of their normals, such as e, f in (i) to the north pole of the sphere. The existence of these underneath normals is indicated by circles which are included in (iii), overlapping the dots in the stereogram which correspond to the upper faces of the crystal.
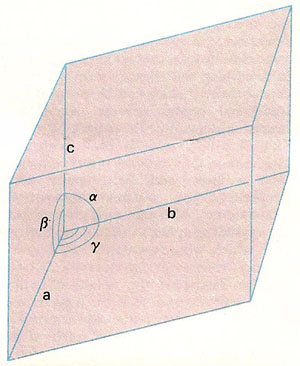
Figure 7. The unit cell of a triclinic crystal, conventionally drawn to show the crystallographic axes a, b, c and the angles α, β, γ between them.

Figure 8. The seven crystal systems.
A crystal is any substance that has solidified in a definite geometrical form. The visible orderly arrangement of crystal faces reflects a similar orderly arrangement of atoms or molecules, making up the substance, at a very tiny scale. The study of crystals is known as crystallography.
Most solid substances, when pure, will form crystals. Solids that don't are said to be amorphous. Crystals are classified according either to the structure of their lattices (e.g., cubic or hexagonal), or the type of chemical bond that holds them together, i.e., ionic crystals, covalent crystals, or metallic crystals. There are also such things as liquid crystals.
Large scale appearance of crystals
Most solids are crystalline to a large degree, and although many solids may appear very imperfect on a macroscopic scale, and quite different from the large crystals seen in mineralogical collections of museums, nevertheless they are almost invariably built up of crystalline regions. In an ordinary piece of metal, for example, these crystalline regions may be invisible to the unaided eye but can be distinguished in a microscope.
Crystals have always fascinated people, and scientists have studied them in detail for several centuries. One of the earliest scientific investigators of crystals was the Danish geologist and anatomist Nicolaus Steno (1638–1686), who carried out studies of quartz in 1669. A century later the French mineralogist Romé de l'Isle (1736–1790), and the Abbé Haüy (1743–1842) made comprehensive measurements of the geometry of a wide variety of crystals.
Good specimens of crystals have well-formed faces that occur in characteristic angular positions. In most crystals the faces are very unevenly developed, making it hard to distinguish the underlying symmetry. The sizes of the individual faces depend on chance circumstances which determine the way the crystal has grown in different directions, but when idealized the crystals have regular shapes. These shapes may be a combination of simpler individual forms, such as a pyramid with a vertical prism, or several different prisms and pyramids. Measurements of the angular inclinations of the various faces of a particular crystal species reveal that they occur at specific angles. The situation is reminiscent of that seen in a well-planned orchard of fruit trees, where we notice that only at a few special viewpoints do the trees fall into lines.
Symmetry in crystals
If we look in more detail at a collection of crystal models we find that it includes representatives of a number of different types of symmetry. For example, there's the highly developed symmetry of the cubic system; crystals of this class are often metals or simple ionic compounds, such as sodium chloride (table salt). A much lower type of symmetry is expressed by crystals belonging to, say, the monoclinic system, which cannot be described in terms of three mutually perpendicular coordinate axes. The monoclinic system has many representatives among organic materials.
Comparing the cubic and monoclinic systems, as represented by metals and organic molecules respectively, illustrates an important concept. When identical spherical atoms or atoms of similar size are packed together a highly symmetrical structure is likely to arise. On the hand, when anisotropic shapes, such as the flat molecules which often occur among organic compounds, are packed together then the resulting symmetry is likely to be much lower. The difference in the symmetries of the solids which occur in these two cases can be compared with the difference, on a much larger scale, between the regular packing which exists in a pile of ball-bearings and the stacked arrangement which is produced when we try to pack together a collection of cards.
Crystal lattices
The regularity of crystal shapes and the fact that they can be split into equally regular fragments suggests that a crystal is constructed of 'units' arranged in a very orderly manner. The idea was first put forward by Haüy as long ago as 1784. He took hundreds of tiny blocks and piled them into cubes, octahedral, and other shapes commonly found amongst crystals. But he did not venture to guess what the basic building blocks of crystals really were.
We now know that the basic 'units' in the structure of a crystal are simple arrangements of either atoms, molecules, or ions. A crystal of sodium chloride (common salt or halite) contains equal numbers of sodium ions and chloride ions. The ions are arranged in a regular, repeating pattern called a lattice. In the case of sodium chloride the simplest unit, which repeats over and over again throughout the lattice, is a cube having sodium ions at four of its corners and chloride ions at the remaining four corners (Figure 4). Because the arrangement is difficult to draw and difficult to visualize the actual ions are usually left out and only their centers are shown. If the centers are joined by straight lines the skeleton of a cube results. Consequently sodium chloride is said to have a simple cube lattice. This does not mean that the entire lattice is necessarily in the shape of a cube, merely that each unit in the lattice has a cubic skeleton.
Copper crystals, too, are built up from a lattice of cubes (Figure 5). But the corners of each cube in this lattice are occupied by atoms of copper, not ions as in common salt. Also, the cube has a copper atom at the center of each face as well as at each corner. Copper is said to have a face-centered cubic lattice. Dry ice (solid carbon dioxide) has a face-centered cubic lattice with molecules (each consisting of a carbon atom merged with two oxygen atoms) occupying the lattice positions.
At temperatures above 906°C iron has a crystal structure like that of copper (i.e. a face-centered cubic lattice). At lower temperatures iron has a body-centered cubic lattice in which each repeating unit consists of eight iron atoms occupying the eight corners of a cube with a ninth iron atom situated at the center of the cube The three different cubic lattices (a simple, face-centered and body-centered) all give rise to crystals of the cubic system. Altogether there are 14 possible crystal lattices, which between them give rise to the seven systems of crystals mentioned earlier.
Why are there are many as 14 possible crystal lattices? The lattice of a particular crystal is determined by several factors. One factor is the different sizes of the atoms, molecules, or ions it contains (in sodium chloride, for example, the chloride ions are almost twice as big as the sodium ions). Another factor is the number of each kind of atom, molecule, or ion contained in the lattice. Sodium chloride contains equal numbers of sodium ions and chloride ions. Calcium fluoride (fluorspar or fluorite) on the other hand has twice as many fluoride ions as calcium ions.
The factor which is most important in determining the lattice arrangement for a particular crystal is the type of bond holding adjacent atoms, molecules, or ions together. For example, pure graphite (the soft gray material used in the 'lead' in pencils) and diamond are chemically identical. Both contain only atoms of carbon. Yet one is hard and one is soft. Each of the atoms in a diamond is linked to four neighboring atoms by precisely the same kind of bond that links atoms in a true molecule (i.e. by sharing each other's outer electrons). In graphite each carbon atom is joined to three neighbors in a flat sheet by sharing electrons, and to a fourth neighbor, not in the same flat sheet, by a much weaker bond. Because of this different kind of bond, graphite has a different kind of lattice from diamond and hence it has different physical properties.
Crystal classes and systems
As a result of extensive study of the external forms of crystals, crystallographers have developed methods of formal classification.
Crystals may be idealized by representing their faces by a system of normals drawn perpendicular to the faces (Figure 6). Then, as a further refinement these normals are represented by points at which they intersect the surface of a sphere. The problem then is to study the arrangement of such collections of points since the symmetry of this arrangement represents the symmetry of the crystal.
In fact there are found to be 32 possible combinations of symmetry elements passing through a point and they are called the 32 point groups. These 32 arrangements can be divided into 7 symmetry systems (Figures 1 and 8), the division being made according to the systems of coordinates to which they can be related. These systems are as follows:
We can therefore list the parameters which are necessary in order to give a full description of a crystal belonging to each of these systems as follows:
In order to examine the way in which these 32 crystal classes are distributed among the 7 systems of crystal symmetry it is convenient to use a method of representing direction which is known as the stereographic projection (Fig 6iii).
Properties of crystals
The size and configuration of crystals in a metal affect its mechanical properties: stress behavior, fatigue, and resistance depend on the crystals. Impurities in the lattice, in concentrations of only a few parts per billion, account for the electrical properties of semiconductors. The magnetic properties of many materials are influenced by the internal disposition and shapes of crystals. Some crystals respond to vibrations by generating electricity by the piezoelectric effect – the principle behind some record-player pickups; the converse is used in ultrasonic transducers and radio-tuning and clock-tuning crystals.
Optical properties of crystals
The transmission of light by crystals differs from that by glass since the refractive index may depend on the direction of incidence of the light (crystals are not in general isotropic). Uniaxial crystals (belonging to the tetragonal, hexagonal, and trigonal systems) have two principal refractive indices and display double refraction. Biaxial crystals (orthorhombic, monoclinic, triclinic) have three principal refractive indices.
Transparent crystals of all systems except the cubic rotate the plane of polarized light. Polaroid polarizing sheets or glasses, as used in sunglasses, contain very small oriented crystals.


