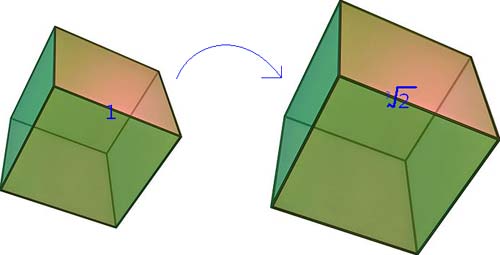
Duplicating the cube is a classical mathematical challenge of antiquity: using only a straightedge and compass, construct a cube whose volume is exactly twice that of a given cube. It is often called the "Delian" problem because of a legend that surrounds its origin.

 

The citizens of Athens were being devastated by a plague so that, in 430 BC, they sought advice from the oracle at Delos on how to rid their community of this pestilence. The oracle replied that the altar of Apollo, which was in the form of a cube, had to be doubled in size. Thoughtless builders merely doubled the edges of the cube, failing to appreciate that this increased the volume of the altar eightfold. The oracle said the gods had been angered; the plague grew worse. Other delegations consulted Plato. When informed of the oracle's admonition, Plato told the citizens "the god has given this oracle, not because he wanted an altar of double the size, but because he wished in setting this task before them, to reproach the Greeks for their neglect of mathematics and their contempt of geometry."

 

Many Greek mathematicians attacked the problem. All failed, because the so-called Delian constant, the cube root of 2 (the required ratio of sides of the original cube and that to be constructed), needed for the duplication can't be constructed as prescribed. Cube duplication is possible, however, using a Neusis construction.