equipotential surface
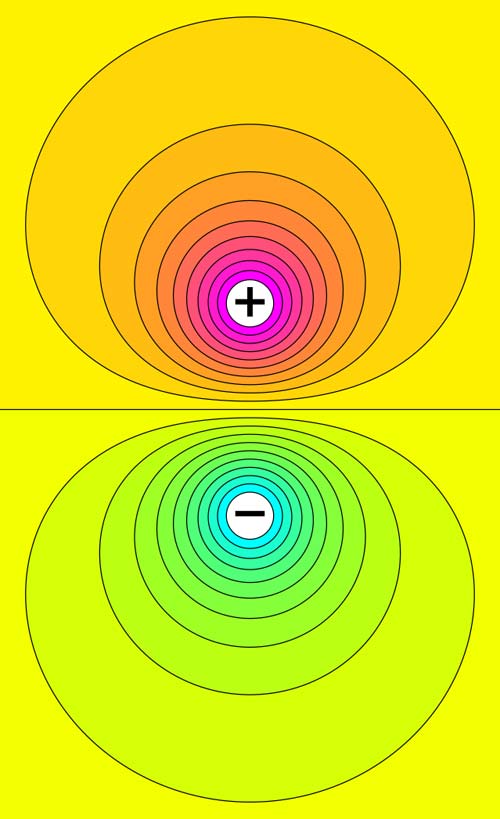
Computed electrostatic equipotentials (black contours) between two electrically charged spheres.
An equipotential surface is a surface surrounding a body, or group of bodies, over which the electrical or gravitational field is of constant strength and, at all points, is directed perpendicular to the surface.
The concept of the critical equipotential surface, popularly known as the Roche lobe, is often misunderstood and applied incorrectly. This equipotential surface arises from the solution of the restricted three-body problem; it describes the gravitational field experienced by a massless body in the vicinity of two point masses orbiting each other in a perfect circle, in the absence of any other force such as radiation pressure or stellar wind. Unless the restricted three-body conditions are met, the surface doesn't exist mathematically. Since there are probably not any binaries with perfect circular orbits, the restricted three-body solutions are at best approximations to real binaries. The use of the term Roche lobe encourages the idea of a kind of impenetrable container from which material can only escape through the gravitationally neutral inner-Lagrangian point. But this is a faulty notion. Earth, for instance, has an infinite number of equipotential surfaces, yet air carries molecules through those surfaces freely. However, the concept of the critical Roche equipotential surface can be useful in understanding the evolutionary processes in close binary stars. It defines an approximate boundary within which the atmosphere of the evolving star can expand while still remaining a distinctly separate object. If that rough boundary is exceeded, the expanding atmosphere will have access to the domain containing both stars.


