harmonics
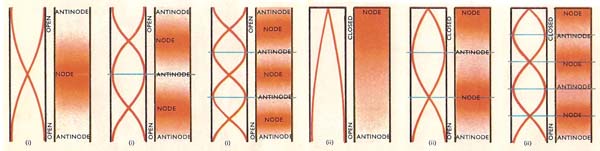
Figure 1. Open organ pipes (i) always have antinodes (where the air molecules vibrate most vigorously) at their open ends and can make all the possible harmonics (2nd, 3rd, 4th, etc.), whereas closed ones (ii) which must have nodes (where the air molecules are at rest) at their closed ends can only give odd-numbered harmonics (3rd, 5th, etc.)

Figure 2. Harmonics. (A) The first 16 modes of harmonic vibration of a stretched string. (B) The musical pitches these would sound if the fundamental (first harmonic) sounded C. (C) The ratios between the frequencies of the different modes of vibration. Thus, the frequency of the fundamental is half (1:2) that of the first overtone (second harmonic) and one-third that of the second overtone (third harmonic); that of the second overtone is two-thirds that of the third overtone, and so on. Note that after the fundamental (the first harmonic), the nth overtone is the (n + 1)th harmonic.
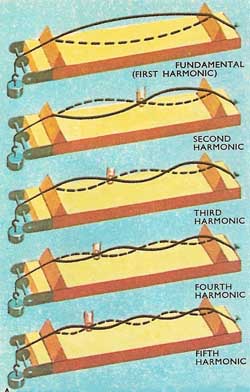
Figure 3. A sonometer. The top wire is sounding its fundamental note, the others are sounding their 2nd, 3rd, 4th, and 5th harmonics.
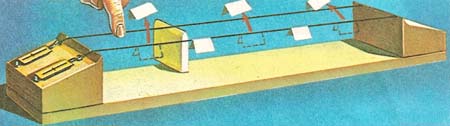
Figure 4. This sonometer has two identical wires. A bridge is placed one third the way along the back wire thereby stopping the wire from moving and forming a node. The shorter section of this wire is plucked in the middle. The front wire vibrates in sympathy. Pieces of paper jump off this wire at antinodes (maximum vibration) and stay on at nodes (no vibration).
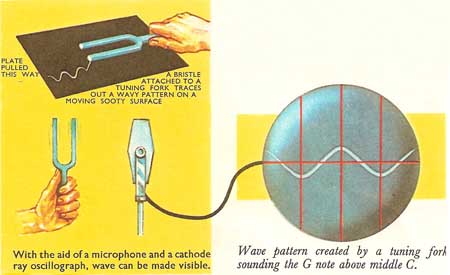
Figure 5. the vibration of a tuning fork made visible on an oscilloscope.
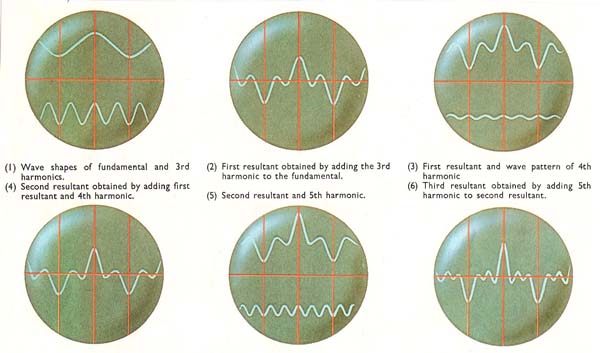
Figure 6. The waves show how the complicated wave pattern of the G note of the clarinet is built up by combining the fundamental with its various harmonics. The shape of the final pattern is largely determined here by the addition of the fundamental and third harmonics (the second harmonic is absent). The 4th and 5th harmonics only slightly alter the wave shape.
Harmonics are vibrations at frequencies which are integer multiples of that of a fundamental vibration: the ascending notes C, G, E, C', E', G' comprise a fundamental with its first five higher harmonics. Apart from their musical consonance, they are important because any periodically repeated signal – a vowel sound, for example – can be produced by superposing the harmonics of the fundamental frequency, each with the appropriate intensity and time lag.
Introduction
Music would be unimaginably dull if all musical instruments playing a certain note – say middle C – were to sound exactly alike. A trumpet and a violin would produce indistinguishable sounds and there would be no point in making different musical instruments. Both of these instruments are capable of producing the same note and yet sound completely different. They make the air around them vibrate with a certain frequency. In the case of middle C, this is at 256 vibrations per second. The basic vibration with the largest possible wave size is called the fundamental. The best known instrument capable of producing the fundamental without producing additional waves is the tuning fork (which is used for tuning pianos) and because of this gives out a very "tinny" note. Additional sound waves give the body or quality to musical notes. These additional sound waves are called harmonics.
When a note is played, fundamental vibrations are set up and also harmonics or overtones. A vibration with a wave half as long as the fundamental is called the second harmonic; a vibration with a wave one-third as long is called the third harmonic and so on (Fig 3 and 4). The different sound qualities of instruments depend on the fact that together with the fundamental, or first harmonic, certain other harmonics are played, some more loudly than others.
Wave forms on an oscilloscope
Pictures of the wave forms of sounds can be obtained by using an electronic apparatus called the cathode ray oscilloscope (Fig 5 and 6). It gives a still picture of wave forms that really are repeating hundreds or thousands of times a second. The picture will be of a very complicated wave which is a combination of the fundamental and various harmonics and will need to be unscrambled by a mechanical harmonics analyzer into simpler waves, one representing each harmonic.
Harmonics and sound quality
The harmonics of some waves are so faint that they can be ignored. In the case of a clarinet, playing the note G above middle C, the first and third harmonics are the most important, the fourth and fifth are of lesser importance. The second harmonic is almost undetectable.
Two different types of organ pipes playing the same note produce different sounds due to the presence of different harmonics or overtones (Figure 1). The two types of organ pipes are the open organ pipe which has both ends open and produces antinodes (places where vibrations are largest) at each end, and the closed organ pipe which produces an antinode at the open end and a node (place of no vibration) at the closed end.
Diagram (i) in Figure 1 shows how the air in an open organ pipe can vibrate in a number of ways, in each case keeping an antinode at each end. The simplest method of vibration occurs when there is just one node, half way along the pipe. The sound produced by this vibration is the fundamental or first harmonic. At the same time the air in the pipe can vibrate so that there are two nodes, one-quarter and three-quarters the way along the pipe. This gives rise to the second harmonic – a sound whose wavelength is half that of the fundamental. The same pipe can also produce third, fourth, fifth, and higher harmonics.
Diagram (ii) shows how the air in an organ pipe closed at one end can vibrate in a number of ways, in each case keeping a node at the closed end and an antinode at the open end. With just one node and one antinode and pipe sounds in the fundamental note or first harmonic. With a second node one-third of the way up the pipe the sound produced has a wavelength of one-third that of the fundamental. This gives to the third harmonic. A closed pipe has no second harmonic – it has only odd-numbered harmonics. Because it lacks even-numbered harmonics the closed organ pipe gives a sound of different quality from the open-ended pipe, though their fundamental notes may be the same.
Harmonics or overtones are what makes the violin sound different from the euphonium. They give the notes their distinctive quality.


