information theory

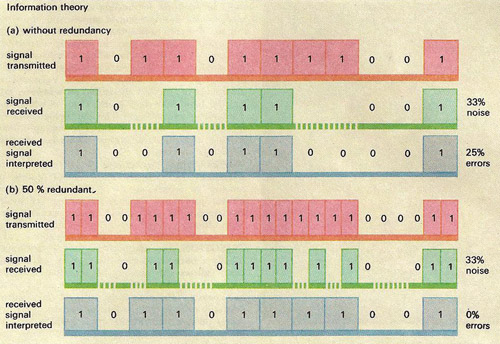
Information theory: How a measure of redundancy in the transmission of a message can improve the probability of its being correctly interpreted on reception. In (A), a simple message in binary digits is transmitted, losing 33% of its information in transmission; on receipt 25% of the message is incorrectly interpreted. (B) By transmitting the message with 50% redundancy, i.e., with each digit repeated, and the same loss in transmission, sufficient information is received for the original message to be correctly reconstructed.

A mathematical theory of information born in 1948 with the publication of Claude Shannon's landmark paper, "A Mathematical Theory of Communication". Its main goal is to discover the laws governing systems designed to communicate or manipulate information, and to set up quantitative measures of information and of the capacity of various systems to transmit, store, and otherwise process information. Among the problems it treats are finding the best methods of using various communication systems and the best methods for separating the wanted information, or signal, from the noise. Another of its concerns is setting upper bounds on what it is possible to achieve with a given information-carrying medium (often called an information channel). The theory overlaps heavily with communication theory but is more oriented toward the fundamental limitations on the processing and communication of information and less oriented toward the detailed operation of the devices used.

The information content of a message is conventionally quantified in terms of bits (binary digits). Each bit represents a simple alternative – in terms of a message, a yes-or-no; in terms of the components in an electrical circuit, that a switch is open or closed. Mathematically the bit is represented as 0 or 1. Complex messages can be represented as a series of bit alternatives. Five bits of information only are needed to specify any letter of the alphabet, given an appropriate code. Thus able to quantify information, information theory employs statistical methods to analyze practical communications problems. The errors that arise in the transmission of signals, often termed noise, can be minimized by the incorporation of redundancy. Here more bits of information than are strictly necessary to enclose a message are transmitted, so that if some are altered in transmission, there is still enough information to allow the signal to be correctly interpreted. Clearly, the handling of redundant information costs something in reduced speed of or capacity for transmission, but the reduction in message errors compensates for this loss. Information theoreticians often point to an analogy between the thermodynamic concept of entropy and the degree of misinformation in a signal.

Related category

• COMPUTERS, ARTIFICIAL INTELLIGENCE, AND CYBERNETICS

Also on this site:

Encyclopedia of Alternative Energy & Sustainable Living
Encyclopedia of History

BACK TO TOP