large numbers


Fig 1. It's easy to grasp at a glance how many spots are on a die.

Fig 2. Even without the numbers marked on playing cards we can instantly recognise their value.
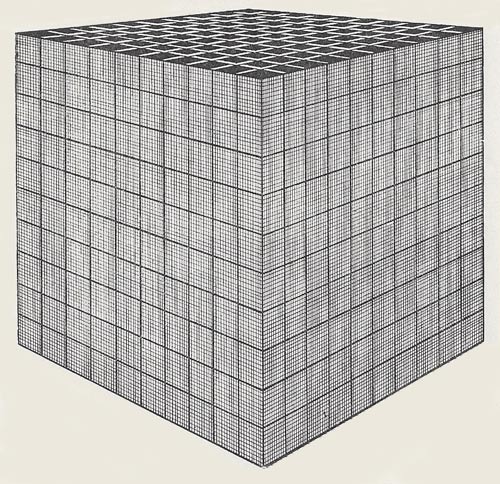
Fig 3. A large cube made of a million small cubes (100 by 100 by 100).
Bigger than the biggest thing ever and then some. Much bigger than that in fact, really amazingly immense, a totally stunning size, real 'wow, that's big,' time... Gigantic multiplied by colossal multiplied by staggeringly huge is the sort of concept we're trying to get across here.
—Douglas Adams, The Restaurant at the End of the Universe
Making, naming, and representing very large numbers is itself a big problem. A simple way to start is by adding zeros: 10, 100, 1,000, 10,000, ..., 1,000,000, ... But this quickly gets tedious and exponentiation becomes a more attractive option: 101, 102, 103, ..., 106, ... Naming the various powers of 10 follows a regular pattern of prefixes. In the United States, 103 is one thousand, 106 is one million, 109 is one billion, 1012 is one trillion, 1015 is one quadrillion, and so on. The "-illion" root kicks in at the sixth power of 10 prefixed by "m" for "mono"; then, every jump of three powers (factor of a thousand) comes the next prefix. Put another way, the US name for 103n uses the Latinized prefix for n-1. One centillion, which is the largest number with a single-word name in English, is 10303. Elsewhere in the world, "billion," "trillion," and so on, can mean other things than they do in the American system. A British billion, for example, is one million million, or 1012, while the now largely-obsolete term milliard was used for a thousand million. However, the American forms have become fairly standard internationally and will be used without qualification in this book. It's also worth noting that, while "quadrillion," "quintillion," etc, are perfectly valid terms, "one thousand trillion," "one million trillion," and so forth, are generally preferred.
100 and counting...
Thousand
Thousand is a number that, linguistically, comes from an extension of "hundred" and has roots in the Germanic teue and hundt. Teue refers to a thickening or swelling, and hundt is the source of our present-day hundred. A thousand, then, literally means a swollen or large hundred. The root teue is the basis of such common words today as thigh, thumb, tumor, and tuber. One thousand is the answer to the question: If you were to spell out numbers, how far would you have to go until you would find the letter "A"? While Americans may say "Thanks a million" to express gratitude, Norwegians offer "Thanks a thousand" ("tusen takk").
Million
One million is a thousand thousand – 1,000,000 or 106. The word comes from the Latin mille for thousand (which is also the root for 'mile' and 'millennium') and the suffix ion that implies 'large' or 'great;' thus a million is literally a 'great thousand.' Although 'million' seems to have come into use as early as the middle of the fourteenth century, most mathematicians would use the phrase 'thousand thousands' to avoid confusion and it was not until the 1700s that 'million' caught on. It appears in the King James version of the Bible (Genesis 24:60) and in Shakespeare (Hamlet act II scene II) – "for the play, I remember, pleased not the million."
Trillion
In American and general usage, a trillion is a million million – 1,000,000,000,000 or 1012. A European trillion is a million times larger than this, or 1018. Counting one number every second, 24 hours a day, it would take 31,688 years to reach one (American) trillion. The first trillion-dollar lawsuit ($116 trillion) was filed in August 2002 by 600 family members against a company run by Osama bin Laden's family, Saudi Arabian princes, and Sudan.
Myriad
'Myriad' is a term which today is normally synonymous with 'very large number.' Its origins go back to the Greek word murious, meaning uncountable. The plural of this, murioi, evolved into the Latin myriad, which the Romans used to represent ten thousand. Myriapod is a general name for any many-legged arthropod, such as a millipede or a centipede.
Getting a feel for large numbers
The meaning of small numbers is easily grasped – as, for instance, the number of dots on the face of a die (Fig 2). Similarly, we can recognise the value of cards up to 10 even if the numbers are not printed on the cards (Fig 3). But we can't accurately tell the number of large collections of things at a glance. When large numbers are involved, it's helpful if the objects are arranged in regular groups. Suppose, for example, we need to count the number of small cubes in a pile.
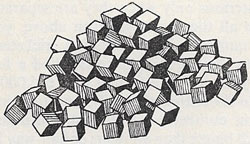 |
We should begin by arranging these in groups ten, with as few odd ones left over as possible. Then we'd group the tall piles into a group of 100 with some tens and units left over.
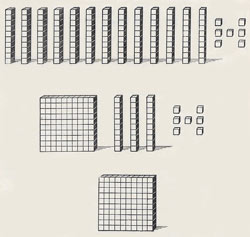 |
Just as a square of 10 by 10 small cubes makes a hundred. So a cube made of 10 by 10 by 10 small cubes makes a thousand.
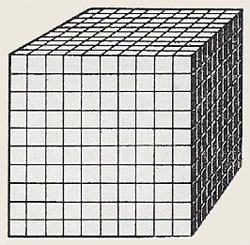 |
A large cube made of 100 by 100 by 100 small cubes contains a million small cubes altogether (Fig 3).
The googol, googolplex, and beyond
Exponentiating quite small numbers seems at first to be a pretty economical way of making and writing large numbers: 1030, for example, is a highly effective shorthand for 1,000,000,000,000,000,000,000,000,000,000. But this method runs out of steam as the numbers get bigger and bigger. Take, for instance, the googol and the googolplex. One googol is the unofficial name for 10100, or 1 followed by 100 zeros. This innocuous-looking number is larger than the number of atoms in the universe. What happens, therefore, if we want to represent the number that is 1 followed by a googol number of zeros? One way would be to write "1 followed by a googol number of zeros"! But this is cheating because it couldn't be generalized without first giving a proper name to a ridiculously large number of numbers. A better solution is to exponentiate using large numbers. Thus, 1 googolplex = 10googol = 1010^100. This is the beginnings of a power tower.
Useful big numbers
Are numbers as large as the googol, not to mention the googolplex, of any practical importance? Science has given us such colossi as Avogadro's number (the number of molecules in a sample whose weight in grams equals its molecular weight) = 6.023 × 1023, the Eddington number (astrophysicist Arthur Eddington's best estimate of the number of protons in the universe) = 1.575 × 1079, and the Supermassive Black Hole Evaporation Time = 10100 years (or thereabouts) – which brings us to the level of the googol. But there's nothing known or that can be reasonably conjectured in the "real" world of physics that goes much beyond this. Science fiction can carry us a bit further. In The Hitchhiker's Guide to the Galaxy,1 by Douglas Adams, appears one of the largest numbers ever used in a work of fiction: 2276709. These are the odds quoted against the characters Arthur Dent and Ford Prefect being rescued by a passing spaceship just after having been thrown out of an airlock. As it happens, they are rescued – by a spaceship powered by the "infinite improbability drive." By contrast, some special numbers in mathematics make even the googolplex look tiny. Skewes' number, 1010^10^34, was long held up as an example of a googolplex-dwarfing number that nevertheless served a bona fide purpose in mathematics. However, even this seemingly immense integer is made to look ridiculously small by the likes of more recently described numbers, such as Graham's number, the Mega, and the Moser, which are so utterly vast that it takes several pages just to describe the various special notations used to represent them.
Just as writing out a number "in full," or in place-value notation, becomes unwieldy with numbers as big as a googol, so exponentiation, in turn, endangers the world's forests if it tries to take on seriously large numbers. A more effective shorthand is tetration – "tetra" (from the Greek meaning "four") because it is the fourth dyadic operation in the series: addition, multiplication, exponentiation, tetration. Dyadic means that two numbers, or arguments, are involved in the operation. Multiplication is repeated addition (e.g., 2 × 3 = 2 + 2 + 2), exponentiation is repeated multiplication (e.g., 23 = 2 × 2 × 2), and tetration is repeated exponentiation. For example, 2 tetrated to 3, represented as 32, is 22^2 = 24 = 16; 2 tetrated to 4, or 42, is 22^2^2 = 216 = 65,536; and 2 tetrated to 5, or 52, is 22^2^2^2 = 265,536 = something too big to write out in full. Tetration goes by various other names including superpower, superdegree, and, the one used most commonly in mathematical circles and also here from now on, hyper4.
New ways of writing seriously large numbers
Just as the exponentiation of two numbers, a and b, is represented as ab and defined as a × a × ... × a (b terms), the hyper4 of a and b is represented as a(4)b and defined as aa^a^...^a (a power tower with b levels). Alternatively, the hyper4 operator can be represented in Knuth's up-arrow notation as a ↑↑ b. Continuing this pattern:
hyper5 of a and b = a(5)b = a(4)a(4) ... a(4) = a ↑↑↑ b
hyper6 of a and b = a(6)b = a(5)a(5) ... a(5) = a ↑↑↑↑ b
hyper7 of a and b = a(7)b = a(6)a(6) ... a(6) = a ↑↑↑↑↑ b
To get some idea of the potency of this kind of representation, consider the sequence
1,
10,
10000000000,
10000000000000000000000000000000000000000000000000000000000000
000000000000000000000000000000000000000, (100 zeroes)
...
Notice how big even the fourth term is? The seemingly innocuous-looking number 5 ↑↑↑↑↑ 5, or 5(7)5, is so huge that it would be around the 100,000,000,000,000,000th (one hundred thousand trillionth) term of this sequence!
Since the dyadic operators discussed above form a pattern, they can be telescoped into a single triadic operator that has three arguments. This can be defined as:
hy(a, n, b) = { 1 + b for n = 0
{ a + b for n = 1
{ a × b for n = 2
{ a ↑ b for n = 3
{ a ↑ hy(a, 4, b – 1) for n = 4
{ hy(a, n – 1, hy(a, n, b – 1))
for n > 4
{ a for n > 1, b = 1
Beyond hyper are other triadic operators capable of generating large numbers even faster. The Ackermann function and the Steinhaus-Moser notation are both equivalent to a triadic operator that is somewhat more powerful than hy(a, n, b). Similarly, Conway's chained-arrow notation marks an evolution of Knuth's symbolism. These various techniques and notations can produce immense finite numbers. But beyond any of these, lie the many different kinds of infinity.
Reference
1. Adams, Douglas. Hitchhiker's Guide to the Galaxy. New York: Ballantine, 1995.


