John Napier was a Scottish mathematician and theological writer who invented logarithms and wrote Mirifici logarithmorum canonis descriptio (1614), which contains the first logarithmic table and the first use of the word logarithm. He also introduced the decimal point in writing numbers. His Rabdologiae (1617) describes various shortcuts for carrying out arithmetical calculations. One method of multiplication uses a system of numbered rods called Napier's rods, or Napier's bones (see below) – a major improvement on the ancient system of counters then in use. In 1619, after Napier's death, his Mirifici logarithmorum canonis constructio, which gave the method of construction of his logarithms, was published by his son Robert and edited by Henry Briggs.

 

 

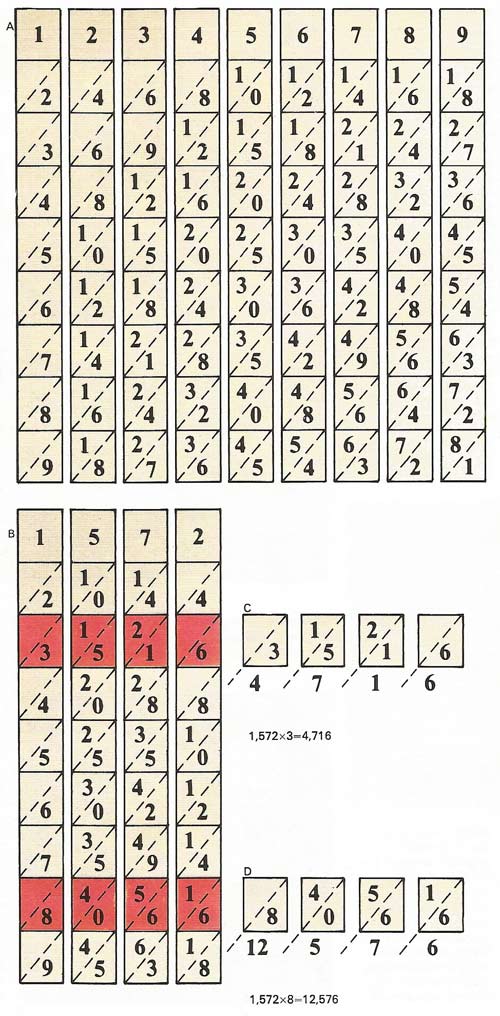
Napier's bones

A practical form of Napier's ideas about logarithms was a set of numbered rods, or bones, that could be used for carrying out multiplication by using the mathematical operation of addition (see illustration right). As with logarithms (and the slide rule) they made use of two types of mathematical series,, called arithmetic and geometric. Napier's bones consisted of a set of nine square-section rods [A] housed in a tray (see below). They were numbered 1 to 9 in the first segment and the lower segments on each rod were divided diagonally. These segments were numbered down the rods in arithmetic series, the "one" rod numbers increasing by 1 (to give 1, 2, 3, 4, and so on), the "two" rod by 2 (2, 4, 6, etc), the "three" rod by 3 (3, 6, 9, etc) and so on for the whole set ending with the "nine" rod which was calibrated in nines (9, 18, 27, 36, etc). The other faces of each square rod were similarly calibrated, so hat each number (1 to 9) had to be represented four times somewhere in the set. To find the multiples of a number – for example 1,572 – the rods numbered 1, 5, 7, and 2 are removed from the tray and laid side by side [B]. To find 3 × 1,572 the third row of rod segments is used, as at C. The numbers displayed can be added diagonally as shown, to yield 4,716, which is the required product. To find 8 × 1,572 the segments in the eighth row are used, as at D. When added diagonally, the numbers displayed this time add to 12,576 – again the required product. To multiply by a larger number, say 38, the appropriate products are merely added together (47,160 – a zero is added because we are now multiplying by 30 not 3 – and 12,576) to give 59,736.