perspective

Figure 1. An lllustration and accompanying description from On Paining (1435) by Leon Battista Alberti, demonstarting his technique for creating perspective in an artwork.
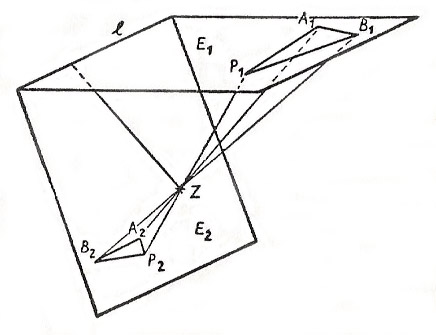
Figure 2. Perspective transformation.
Two figures or solid bodies that arise from one another by a perspective transformation are said to be in perspective with respect to one another. The perspective image of a circle can, for example, be a parabola, and the parabola and the circle are then in perspective with respect to one another.
Linear perspective in painting
Linear perspective occurs when , in a two-dimensional image such as a painting, converging lines meet at a single vanishing point, with all objects in the scene becoming smaller and smaller the farther away they are in the background image, according to a set scale. The idea was first written about by the Italian architect, author, and priest Leon Battista Alberti (1404–1472) in his book On Painting (1435), generally considered to be the world's first modern treatise on to how to represent accurately three-dimensional images on a two-dimensional surface, such as a wall or canvas.
The problem of perspective had been looming for a while. After hundreds of years of overtly religious art devoted mostly to heavenly figures, artists in the Renaissance changed their focus to the world around them. Buildings, towns, and everyday objects began to appear in pictures, and all of a sudden it became prudent for an artist who was interested in realistically depicting the world to try to figure out how to paint landscapes and streetscapes so that the paintings resembled what the viewer actually saw in real life.
Most artists working in Europe after 1435 were aware of Alberti's seminal work. Beginning with a "stage" area in the picture's foreground, he then drew a kind of receding grid on which all the other elements in the painting would be arranged , using the viewer's height as a guide. This was not the first time a creative artist had identified and tried to make sense of perspective, however. The architect Filippo Brunelleschi (1377–1446) had suggested a solution some years earlier, but the particulars of his approach were never properly understood. Alberti's grid showing a proper understanding of perspective and how to achieve it. His work had a profound impact on Renaissance painting(c. 1450–1600), and his principles still form the basis of linear perspective today.
Perspective transformation
plane perspective transformation
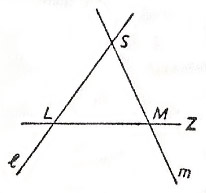
In a perspective transformation in a plane, the points of two different straight lines are associated with one another in the following way:
If l and m are given straight lines and Z is a point of the plane which lies neither on l or m, then a point L of l is associated with the point of intersection, M, of ZL with M (M is the image-point of L). Z is called the perspective center or the center of perspectivity (Fig 3). Thus in a perspective, the image-points on m arise out of the points of l by central projection.
 |
| Figure 3. |
Such a perspective of the points of two straight lines possesses a fixed point (a point whose image coincides with the point itself), namely the point of intersection P of the two lines.
Example of perspective transformation in space
If E1 and E2 are two different planes in space, and Z is a point outside both E1 and E2, a perspective can be defined in the following way.
If P1 is a point of E1 the point of intersection P2 of the line ZP1 with the plane E2 is associated with P1 as its image-point. The points of the line of intersection l of E1 and E2 are fixed points of this transformation (Figure 2).


