rational number
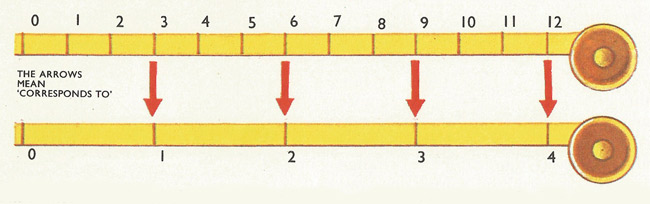
The number line for feet and yards. A number of feet correspond to a number of yards. Three feet correspond to one yard, and so on.
Ordered pairs.

Mapping.
There are many other numbers beside the natural numbers (0, 1, 2, 3,...) and the directed numbers, or integers. The missing numbers lie in the gaps left between the natural numbers (or integers). They are called the rational numbers, because they are defined as ratios (one number divided by another number).
The missing numbers can easily be seen by plotting sets of numbers along the number line. The method also involves mapping one set of numbers on to the set of integers on the number line.
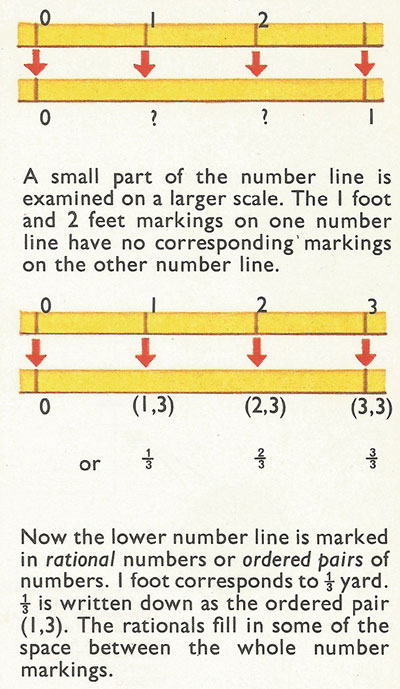
Suppose the upper set represents a distance in feet and the lower set a distance in yards. There are three 'foot' markings to every 'yard' marking. So two out of three foot markings do not correspond to any of the numbers on the yard line. It is obvious that they correspond to a third of a yard. But 1/3 is neither a natural number nor an integer. What kind of number is it? It is often known as a fraction and, if 1 is divided by 3, by the decimal number 0.333... Yet another way of writing the number is as an ordered pair of numbers (1, 3). These are all ways of writing rational numbers.
The ordered pair notation is perhaps the most useful and versatile. Fractions need two numbers (the numerator and denominator of the fraction) to define them. In the usual fractional form, the numbers are set one over the other. In the ordered pair notation, they are set one after the other.
Sets of ordered pairs
The set of rational numbers
1/3, 2/3, 3/3, 4/3,...
have one thing in common. They are all numbers of thirds. 3 is the denominator of each of the fractions. In other words, they all belong to the set of thirds.
In the ordered pairs of notation, the same set is written as
(1, 3), (2, 3), (3, 3), (4, 3),...
Ordered pairs from a useful set when the second number of the pair is the same for each ordered pair. In particular, this simplifies the rules for adding and subtracting the pairs.


