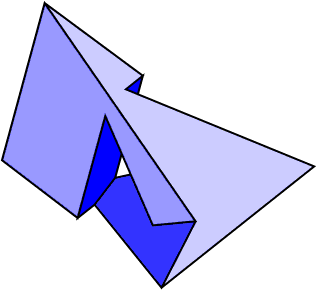
The Szilassi polyhedron is a toroidal heptahedron (seven-sided polygon) first described in 1977 by the Hungarian mathematician Lajos Szilassi. It has 7 faces, 14 vertices, 21 edges, and 1 hole. The Szilassi polyhedron is the dual of the Császár polyhedron and, like it, shares with the tetrahedron the property that each of its faces touches all the other faces. Whereas a tetrahedron demonstrates that four colors are necessary for a map on a surface topologically equivalent to a sphere, the Szilassi and Császár polyhedra show that seven colors are necessary for a map on a surface topologically equivalent to a torus.