tiling
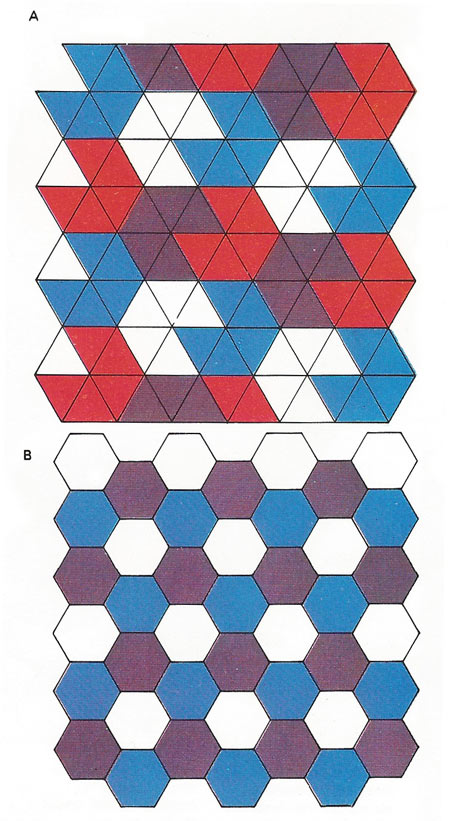
Various polygonal tilings.

Tiling with curved shapes.
A tiling, also called a tesselation, is a collection of smaller shapes that precisely covers a larger shape, without any gaps or overlaps. Usually, the shape to be tiled is a flat plane but other shapes and three-dimensional objects can be tiled, too.
Tiling a floor with identical tiles can be done in various ways (see diagrams to the right). Obviously it can be done with equilateral triangles [A], hexagons [B], squares, or with tiles made by fusing shapes together [C]. But it can not be done with pentagons or any tiles with pentagonal symmetry. Geometry proves that there are just 5 basically different tiling patterns – including the most ornate – using identical tiles.
 |
Games with tilings
In a game that involves tiling, certain conditions are applied; for example, all the tiles may have to be identical, or they may all have to be squares but every one of a different size.
It's been known for some time that all simple regular tilings in the plane belong to one of the 17 plane symmetry groups. All 17 of these patterns are known to exist in the Alhambra palace. This doesn't exhaust the apparently simple problem of tiling the plane: adding extra constraints or removing the requirement for regularity leads to a large number of interesting problems. These include alternating tilings, for examples of squares or dominoes, such that two tiles have a side or a part of a side in common, or colored tilings, in which no two adjacent tiles have the same color.
Colored tilings are also called colored maps. The most famous problem relating to colored tilings was the four-color problem, which has been solved. Other problems involve n-tesselations, in which each tile has an integral area and for each natural number n there is exactly one tile with area n.

