Approximation

Approximation is the setting of an approximate value V_a in place of a true but imprecisely known value V where V – V_a lies within known limits. There are several different ways of expressing approximations and their limits of accuracy. These go by the general name of "rounding".

 

If, for example, we approximate 2.3654202 by 2.365420 we say that this is correct to 6 decimal places, in that the six figures after the decimal point are correct. It is common practice, when approximating to (n – 1) decimal places a number that has n decimal places, to round up if the nth figure after the point is 5 or greater, down if it is less than 5. Thus 3.65 can be written as 3.7 to 1 decimal place; 3.64 as 3.6. For some purposes it is often considered correct to round something 0.5 to the nearest even number, i.e. not always upward). This is known as "banker's rounding". For instance, 5.5 would be rounded to 6 but 12.5 would be rounded to 12. This method avoids introducing a bias to a large set of numbers, by rounding up more or less as often as rounding down.

 

Another way of approximating is in terms significant figures. For example, 2.3654202 can be expressed as 2.365420 to 7, since the first 7 figures are correct, rounding down.

 

An alternative way of writing approximations is by use of the sign ± ("plus or minus"). Thus 2.365420±0.0000004 is an approximation stating that the correct value lies between 2.3654196 and 2.3654204.

 

Approximation is required in almost all computations, due either to inherent inaccuracies in the calculating device or to the technique of calculation, or because greater accuracy is unnecessary. The techniques of approximation to a function are of paramount importance in calculus.

 

The error accumulated during a calculation due to significant figures or, for integer numbers, fewer value-carrying (non-zero) digits. For example, 386.804 may be rounded successively to 386.80, 386.8, 387.390, and 400. Rounding may be carried out in two ways: by rounding down, which is equivalent to truncation, and by rounding up the last digit to be retained by one unit.

 

Decimal places

Main article

 

The decimal place is the number of places to the right of a decimal point required to specify a real number to a certain accuracy.

 

Significant figures

Significant figures, also called significant digits, are the digits that express a number to a desired accuracy. The significant digits of a given number begin with the first non-zero integer digit or, if this number is less than unity, with the first, zero or non-zero, decimal digit. They end with the final, zero or non-zero, decimal digit; the final zero or zeros of an integer may or may not be significant. For example, 2.871828 to six significant figures is 2.87183 (6 s.f.); to three significant figures it is 2.87 (3 s.f.).

 

Average

'Average' is a vague term that usually refers to the arithmetic mean but can also signify the median, mode, geometric mean, or weighted mean. The word stems from a commercial practice of the shipping age. The root aver means to declare, and the shippers of goods would declare the value of their goods. When the goods were sold, a deduction was made from each persons share, based on their declared value, for a portion of the loss or "average."

 

Mean

When she told me I was average, she was just being mean.
    – anonymous

 

The mean is a precisely calculated 'typical' value of a group of numbers. There a several kinds of mean.

 

Arithmetic mean

The arithmetic mean, which is usually what is meant when people talk about an average, is the sum of a set of values divided by the number of values. For example, the arithmetic average of 3, 4, 7, and 10, is (3 + 4 + 7 + 10)/4 = 6.

 

Geometric mean

The geometric mean of n values is the nth root of the product of the values. In the case of two numbers, a and b, the geometric mean is √(ab). Thus the geometric mean of the numbers 4 and 9 is √(4 × 9) = √36 = ±6. If the numbers are 3, 8, and 10 then the geometric mean is (3 × 8 × 10)^1/3 or the cube root of 240.

 

Harmonic mean

The harmonic mean is the reciprocal of – in other words, one over – the mean of the reciprocals of the values. For example, the harmonic mean of 3, 8, and 10 is 1/[(1/3 + 1/8 + 1/10)/3].

 

Weighted mean

If, in a set of observations, the observations are weighted according to their relative reliability, the individual values are first multiplied by weighting factors before they are summed and the mean taken; this is then called a weighted mean.

 

Median

A different kind of average is median, which is generally the center term when a group of numbers are ordered by size. The median is the value of the middle member of a set of numbers when arranged in order from smallest to largest. For example, in the series 2, 3, 7, 9, 10, the median is 7. With an even number of items, the median is taken to be the arithmetic mean of the two middle items. Thus, in the series 2, 3, 7, 8, the median is 5.

 

The words 'mean' and 'median' both come from the same origin – the Indo-European root medhyo meaning 'middle'.

 

Mode

The mode is the most frequently occurring value in a sequence of numbers. For example, if the scores of 10 students in a group are 2, 4, 4, 4, 5, 8, 9, 9, 10, and 10, the mode is 4 because it's the score that occurs most often.

 

Average of a function

The average value A of a function between x = a and x = b is defined as the area under the curve of the function (see calculus) divided by (b – a):

 

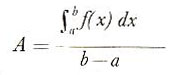
Root-mean-square (RMS)

The RMS is the value obtained by taking the mean of a set of squared values. It provides the value of a periodic quantity and was developed at the beginning of the twentieth century as an accurate measure of voltage and electric current. An RMS error of approximity is also used for equations devised to predict outcomes, such as weather forecasts.

 

difference equation

interpolate
iteration

least squares