abundant number

An abundant is a number that is smaller than the sum of its aliquot parts (proper divisors). Twelve is the smallest abundant number – the sum of its aliquot parts is 1 + 2 + 3 + 4 + 6 = 16 – followed by 18, 20, 24, and 30.

 

A weird number is an abundant number that is not semiperfect; in other words, n is weird if the sum of its divisors is greater than n, but n is not equal to the sum of any subset of its divisors. The first few weird numbers are 70, 836, 4030, 5830, and 7192. It isn't known if there are any odd weird numbers.

 

A deficient number is one that is greater than the sum of its aliquot parts. The first few deficient numbers are 1, 2, 3, 4, 5, 7, 8, and 9. Any divisor of a deficient (or perfect) number is deficient. A number that is not abundant or deficient is known as a perfect number.

 

aleph

Aleph is the first letter of the Hebrew alphabet. It was first used in mathematics by Georg Cantor to denote the various orders, or sizes, of infinity: aleph-null, aleph-one, etc. An earlier (and still used) symbol for infinity, looking like an "8" on its side, was introduced in 1655 by John Wallis in his Arithmetica infinitorum but didn't appear in print until the Ars conjectandi by Jakob Bernoulli, published posthumously in 1713 by his nephew Nikolaus Bernoulli.

 

 

algebraic number

An algebraic number is a real number that is a root of a polynomial equation with integer coefficients. For example, any rational number a/b, where a and b are non-zero integers, is an algebraic number of degree one, because it is a root of the linear equation bx – a = 0. The square root of two is an algebraic number of degree two because it is a root of the quadratic equation x ² – 2 = 0. If a real number is not algebraic, then it is a transcendental number. Almost all real numbers are transcendental because, whereas the set of algebraic numbers is countably infinite, the set of transcendental numbers is uncountably infinite (see infinity).

 

almost perfect number

An almost perfect number is a description sometimes applied to the powers of 2 because the aliquot parts (proper divisors) of 2ⁿ sum to 2ⁿ – 1. So a power of 2 is a deficient number (one that is less than the sum of its proper divisors), but only just. It isn't known whether there is an odd number n whose divisors (excluding itself) sum to n – 1.

 

amicable numbers

Amicable numbers are pairs of numbers, also known as friendly numbers, each of whose aliquot parts add to give the other number. (An aliquot part is any divisor that doesn't include the number itself).

 

The smallest amicable numbers are 220 (aliquot parts 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, and 110, with a sum of 284) and 284 (aliquot parts 1, 2, 4, 71, and 142, with a sum of 220). This pair was known to the ancient Greeks, and the Arabs found several more. In 1636 Pierre de Fermat rediscovered the amicable pair 17296 and 18416; two years later René Descartes rediscovered a third pair, 9363584 and 9437056. In the 18th century Leonhard Euler drew up a list of more than 60. Then, in 1866, B. Nicoló Paganini (not the violinist!), a 16-year-old Italian, startled the mathematical world by announcing that the numbers 1184 and 1210 were friendly. This second lowest pair of all had been completely overlooked. Today, the tally of known amicable numbers has grown to about two and half million. No amicable pair is known in which one of the two numbers is a square. An unusually high proportion of the numbers in amicable pairs ends in either 0 or 5.

 

Arabic numeral

Arabic numerals are numerals written with Arabic digits alone: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, or in combination: 10, 11, 12, ... 594, ... The system actually derives from Hindu mathematics.

 

automorphic number

An automorphic number, also known as an automorph, is a number n whose square ends in n. For instance 5 is automorphic, because 5² = 25, which ends in 5. A number n is called trimorphic if n ³ ends in n. For example 49³, = 117649, is trimorphic. Not all trimorphic numbers are automorphic. A number n is called tri-automorphic if 3n ² ends in n; for example 667 is tri-automorphic because 3 × 667², = 1334667, ends in 667.

 

Bell number

A Bell number is the number of ways that n distinguishable objects (such as differently colored balls) can be grouped into sets (such as buckets) if no set can be empty. For example, if there are three balls, colored red (R), green (G), and blue (B), they can be grouped in five different ways: (RGB), (RG)(B), (RB)(G), (BG)(R), and (R)(G)(B), so that the third Bell number is 5. The sequence of Bell numbers, 1, 2, 5, 15, 52, 203, 877, 4140, 21147,..., can be built up in the form of a triangle, as follows. The first row has just the number one. Each successive row begins with the last number of the previous row and continues by adding the number just written down to the number immediately above and to the right of it.

 

 

The Bell numbers appear down the left-hand side of the triangle. These normal Bell numbers contrast with ordered Bell numbers, which count the number of ways of placing n distinguishable object (balls) into one or more distinguishable sets (buckets) The ordered Bell numbers are 1, 3, 13, 75, 541, 4683, 47293, 545835, ...

 

Bell numbers, named after Eric Temple Bell, who was one of the first to analyze them in depth, are related to the Catalan numbers.

 

See also combinatorics.

 

Bernoulli number

A Bernoulli number is a number of the type defined by Jakob Bernoulli in connection with evaluating sums of the form ∑ i ^k. The sequence B₀, B₁, B₂, ... can be generated using the formula

 

x/(e^x - 1) = ∑(B_n x ⁿ)/n!

 

though various different notations are used for them. The first few Bernoulli numbers are: B₀ = 1, B₁ = –1/2, B₂ = 1/6 , B₄ = –1/30 , B₆ = 1/42 , ... They crop up in many diverse areas of mathematics including the series expansions of tan x and Fermat's last theorem.

 

Betti number

The Betti number is an important topological property of a surface, named after the Italian mathematician Enrico Betti (1823–1892). It is the maximum number of cuts that can be made without dividing the surface into two separate pieces. If the surface has edges, each cut must be a "crosscut," one that goes from a point on an edge to another point on an edge. If the surface is closed, like a sphere, so that it has no edges, each cut must be a "loop cut," a cut in the form a simple closed curve. The Betti number of a square is 0 because it is impossible to crosscut without leaving two pieces. However, if the square is folded into a tube, its topology changes – it now has two disconnected edges – and its Betti number changes to 1. A torus, or donut shape, has a Betti number of 2. See also chromatic number.

 

binary

Main article: binary.

 

cardinal number

A cardinal number is a number, often called simply a cardinal, that is used to count the objects or ideas in a set or collection: zero, one, two, ... , eighty-three, and so on. The cardinality of a set is just the number of elements the set contains. For finite sets this is always a natural number. To compare the sizes of two sets, X and Y, all that's necessary is to pair off the elements of X with those of Y and see if there are any left over. This concept is obvious in the case of finite sets but leads to some strange conclusions when dealing with infinite sets (see infinity). For example, it is possible to pair off all the natural numbers with all the even numbers, with none left over; thus the set of natural numbers and the set of even numbers have the same cardinality. In fact, an infinite set can be defined as any set that has a proper subset of the same cardinality. Every countable set that is infinite has a cardinality of aleph-null; the set of real numbers has cardinality aleph-one. See also ordinal number.

 

Carmichael number

A Carmichael number, aso known as an absolute pseudoprime, a number n that is a Fermat pseudoprime to any base, i.e., it divides (aⁿ – a) for any a. Another way of saying this is that a Carmichael number is actually a composite number even though Fermat's little theorem suggests it is probably a prime number. (Fermat's little theorem says that if P is a prime number then for any number a, (a^P – a) must be divisible by P. Carmichael numbers satisfy this condition to any base despite being composite.)

 

There are only seven Carmichael numbers under 10,000 – 561, 1105, 1729, 2465, 2821, 6601, and 8911 – and less than a quarter of a million of them under 10¹⁶. Nevertheless, in 1994 it was proved that there are infinitely many of them. All Carmichael numbers are the product of at least three distinct primes, for example, 561 = 3 × 11 × 17.

 

Catalan number

A Catalan number is any number, u_n, from the Catalan sequence defined by

 

u_n = (2n)! / (n + 1)!n!

 

It begins: 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, ... The values of u_n represent the number of ways a polygon with n + 2 sides can be cut into n triangles using straight lines joining vertices and are named after the Belgian mathematician Eugène Catalan (1814-1894). They also arise in other counting problems, for example in determining how many ways 2n beans can be divided into two containers if one container can never have less than the second.

 

chromatic number

1. In graph theory, the chromatic number is the minimum number of colors needed to color (the vertices of) a connected graph so that no two adjacent vertices are colored the same. In the case of simple graphs, this so-called coloring problem can be solved by inspection. In general, however, finding the chromatic number of a large graph (and, similarly, an optimal coloring) is an NP-hard problem.

 

2. In topology, the chromatic number is the maximum number of regions that can be drawn on a surface in such a way that each region has a border in common with every other region. If each region is given a different color, each color will border on every other color. The chromatic number of a square, tube, or sphere, for example, is 4; in other words, it is impossible to place more than four differently-colored regions on one of these figures so that any pair has a common boundary. "Chromatic number" also indicates the least number of colors needed to color any finite map on a given surface. Again, this is 4 in the case of the plane, tube, and sphere, as was proved quite recently in the solution to the four-color problem. The chromatic number, in both senses just described, is 7 for the torus, 6 for the Möbius band, and 2 for the Klein bottle. See also Betti number.

 

circular number

A circular number is any number whose powers end on the same figure as it does itself. Circular numbers are numbers ending in 0, 1, 5, or 6.

 

common fraction

A common fraction is any fraction that consists of the quotient of two integers.

 

composite number

A composite number is a positive integer that can be factored into smaller positive integers, neither of which is one. If a positive integer is not composite (4, 6, 8, 9, 10, 12, ...) or one, then it is a prime number (2, 3, 5, 7, 11, 13, 17, ...). As Karl Gauss put it in his Disquisitiones Arithmeticae (1801): "The problem of distinguishing prime numbers from composite numbers and of resolving the latter into their prime factors is known to be one of the most important and useful in arithmetic." One reason it is important today is that many secret codes and much of the security of the Internet depends in part on the relative difficulty of factoring large numbers. But more basic to a mathematician is that this problem has always been central to number theory.

 

Numbers that, for their size, have a lot of factors are sometimes referred to as highly composite numbers. Examples include 12, 24, 36, 48, 60, and 120.

 

computable number

A computable number is a real number for which there is an algorithm that, given n, calculates the nth digit. Alan Turing was the first to define a computable number and the first to prove that almost all numbers are uncomputable. An example of a number that, even though well-defined, is uncomputable is Chaitin's constant.

 

continued fraction

A continued fraction is a representation of a real number in the form

 

 

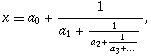which, mercifully for typesetters, can be written in compact notation as

 

x = [a₀; a₁, a₂, a₃, ...]

 

where the integers a_i are called partial quotients. Although rarely encountered in school and even college math courses, continued fractions (CFs) provide one of the most powerful and revealing forms of numerical expression. Numbers whose decimal expansions look bland and unremarkable suddenly turn out, when unfolded as CFs, to possess extraordinary symmetries and patterns. CFs also offer a way of constructing rational approximations to irrational numbers and discovering the most irrational numbers.

 

CFs first appeared in the works of the Indian mathematician Aryabhata in the sixth century, who used them to solve linear equations. They reemerged in Europe in the 15th and 16th centuries and Fibonacci attempted to define them in a general way. The actual term "continued fraction" first appeared in 1653 in an edition of Arithmetica Infinitorum by John Wallis. Their properties were also studied by one of Wallis's English contemporaries, William Brouncker, who along with Wallis, was one of the founders of the Royal Society. At about the same time, in Holland, Christiaan Huygens made practical use of CFs in his designs of scientific instruments. Later, in the 18th and early 19th centuries, Carl Gauss and Leonhard Euler delved into many of their deeper properties.

 

CFs can be finite or infinite in length. Finite CFs are unique so long as we don't allow a quotient of 1in the final entry in the bracket; for example, we should write 1/2 as [0; 2] rather than as [0; 1, 1]. We can always eliminate a 1 from the last entry by adding to the previous entry. If CFs are finite in length then they can be evaluated level by level (starting at the bottom) and will reduce always to a rational fraction; for example, the CF [1; 3, 2, 4] = 40/31. However, CFs can be infinite in length, in which case they produce representations of irrational numbers. Here are the leading terms from a few notable examples of infinite CF:

 

     e = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, ...]
     √2 = [1; 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, ...]
     √3 = [1; 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, ...]
     π = [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, ...]

 

These examples reveal a number of possibilities. All of the expansions have simple patterns except that for pi, which was first calculated by John Wallis in 1685 and has no obvious pattern at all. There also seems to be a preference for the quotients to be small numbers in these examples. The CF for e was first calculated by Roger Cotes, the Plumian Professor of Experimental Philosophy at Cambridge, in 1714.

 

If an infinite CF is chopped off after a finite number of steps then the result is a rational approximation to the original irrational. For example, in the case of π, chopping the CF at [3; 7] gives the familiar rational approximation for π of 22/7 = 3.1428571... Retaining two more terms leads to [3; 7, 15, 1] = 353/113 = 3.1415929..., which is an even better approximation to the true value of π (3.14159265...) and one that was known to the early Chinese. The more terms retained in the CF, the better the rational approximation becomes. In fact, the CF provides the best possible rational approximations to a general irrational number. Notice also that if a large number occurs in the expansion of quotients, then truncating the CF before that will produce an exceptionally good rational approximation. Most CF quotients are small numbers (1 or 2), so the appearance in the CF of π of a number as large as 292 so early in the expansion is unusual. It also leads to an extremely good rational approximation to π = [3; 7, 15, 1, 292] = 103993/33102.

 

cube number

A cube number is a number formed by multiplying a digit by itself three times. Each cube number can be represented by a cube made up of unit cubes (Fig 3).

 

Cullen number

A Cullen number is a number of the form (n × 2ⁿ ) + 1, denoted C_n, and named after the Reverend James Cullen (1867–1933), an Irish Jesuit priest and schoolmaster. Cullen noticed that the first, C₁ = 3, was a prime number, but with the possible exception of the 53rd, the next 99 were all composite. Soon afterward, Cunningham discovered that 5591 divides C₅₃, and noted that all the Cullen numbers are composite numbers for n in the range 2 < n < 200, with the possible exception of 141. Five decades later Robinson showed that C₁₄₁ is a prime. Currently, the only known Cullen primes are those with n = 1, 141, 4713, 5795, 6611, 18496, 32292, 32469, 59656, 90825, 262419, 361275, and 481899. Although the vast majority of Cullen numbers are composite, it has been conjectured that there are infinitely many Cullen primes. Whether n and C_n can simultaneously be prime isn't known. Sometimes, the name "Cullen number" is extended to include the Woodall numbers, W_n = (n × 2ⁿ ) – 1. Finally, a few authors have defined a number of the form (n × bⁿ ) + 1, with n + 2 > b, to be a generalized Cullen number.

 

cute number

A cute number is a number n such that a square can be cut into n squares of, at most, two different sizes. For example, 4 and 10 are cute numbers.

 

cyclic number

A cyclic number is a number with n digits, which, when multiplied by 1, 2, 3, ..., n produces the same digits in a different order. For example, 142857 is a cyclic number: 142857 × 2 = 285714; 142857 × 3 = 428571; 142857 × 4 = 571428; 142857 × 5 = 714285; 142857 × 6 = 857142, and so on. It has been conjectured, but not yet proven, that an infinite number of cyclic numbers exist.

 

decimal

Decimal is the commonly used number system, also known as denary, in which each place has a value 10 times the value of the place at its right. For example, 4327 in the decimal (base 10) system is shorthand for (4 × 10³) + (3 × 10²) + (2 × 10¹) + (7 × 10⁰), where 100 = 1. Similarly, fractions may be expressed by setting their denominators equal to powers of 10.

 

The word decimal comes from the Latin decimus for "tenth." The verb decimare, literally "to take a tenth of," was used to describe a form of punishment applied to mutinous units in the Roman army. The men were lined up and every tenth soldier was killed as a lesson to the rest. From this custom comes our word "decimate," which we use more loosely – in fact, incorrectly – to indicate near-total destruction. The Latin decimare was also used in a less ferocious sense to mean "to tax to the amount of one tenth." However, the usual word describing a one-tenth tax in English is tithe, which comes from the Old English teogotha, a form of tenth.

 

decimal fraction

A decimal fraction is a number consisting of an integer part, which may be zero, and a decimal part less than unity that follows the decimal marker (which may be a point or a comma). A finite or terminating decimal fraction has a sequence of decimals with a definite break-off point after which all the places are zeros. Other fractions produce endless sequences of decimals that are periodic non-terminating.

 

denominator

In a rational number, the denominator is the number that appears below the fraction bar, i.e., the divisor of a common fraction. The denominator indicates how many parts the whole is divided into. For example, in the fraction 3/5, the denominator is 5; 3 is the numerator.

 

duodecimal

Duodecimal is a number system using the powers of 12, which are allotted place values as in the decimal system. The number written in decimals 4092 can be expressed as (2 × 12³) + (4 × 12²) + (5 × 12¹) + (0 × 12⁰) or, in duodecimals, 2450. Fractions are expressed similarly. Two extra symbols are needed for this system to represent the numbers 10 and 11; these are generally accepted as X (dek) and Σ (el) respectively.

 

The advantage of this system can be realized by consideration of the integral factors of 10 and 12: 10 has two (2, 5) while 12 has four (2, 3, 4, 6). The fractions one-third and two-thirds are 0.4 and 0.8, respectively, in duodecimal – much simpler than the recurring expressions 0.3333... and 0.6666... in the decimal system.

 

The most common examples of everyday use of this system are the setting of 12 inches to the foot and 12 months to the year.

 

In 1944 the Duodecimal Society, advocating the use of the duodecimal for scientific purposes, was formed in New York. Although the society still exists, its name has changed to the Dozenal Society of America and the Dozenal Society of Great Britain. The word "dozenal" is used instead of "duodecimal" because the latter comes from Latin roots that express twelve in base-ten terminology.

 

economical number

An economical number is a number that has no more digits than there are digits in its prime factorization (including powers). If a number has fewer digits than are in its prime factorization it is known as a frugal number. The smallest frugal is 125, which has three digits, but can be written as 5³, which has only two. The next few frugals are 128 (2⁷), 243 (3⁵), 256 (2⁸), 343 (7³), 512 (2⁹), 625 (5⁴), and 729 (3⁶). An equidigital number is an economical number that has the same number of digits as make up its prime factorization. The smallest equidigitals are 1, 2, 3, 5, 7, and 10 (= 2 × 5). All prime numbers are equidigital. An extravagant number is one that has fewer digits than are in its prime factorization. The smallest extravagant number is 4 (= 2²), followed by 6, 8, and 9. There are infinitely many of each of these kinds of numbers. Are there also arbitrarily long sequences of consecutive ones? Strings of consecutive economical numbers of length seven start at each of 157, 108749, 109997, 121981 and 143421. On the other hand, the longest string of consecutive frugal numbers up to 1000000 is just two (for example, 4374 and 4375). Even so, it has been proved that, if a certain conjecture about prime numbers, known as Dickson's Conjecture is true, then there are arbitrarily long strings of frugals.

 

equivalent numbers

Equivalent numbers are numbers such that the sums of their aliquot parts (proper divisors) are the same. For example, 159, 559, and 703 are equivalent numbers because their aliquot parts all sum to 57.

 

factorion

A factorion is a natural number that equals of the sums of the factorials of its digits in a given base. The only known decimal factorions are 1 = 1!, 2 = 2!, 145 = 1! + 4! + 5!, and 40585 = 4! + 0! + 5! + 8! + 5!.

 

Fermat number

A Fermat number is a number defined by the formula F_n = 2^{2^n} + 1 and named after Pierre Fermat who conjectured, wrongly, that all such numbers would be prime. The first five Fermat numbers, F₀ = 3, F₁ = 5, F₂ = 17, F₃ = 257, and F₄ = 65,537, are prime. However, in 1732, Leonhard Euler discovered that 641 divides F₅. It takes only two trial divisions to find this factor because Euler showed that every factor of a Fermat number F_n with n greater than 2 has the form k × 2ⁿ⁺² + 1. In the case of F₅ this is 128k + 1, so we would try 257 and 641 (129, 385, and 513 are not prime). It is likely that there are only finitely many Fermat primes.

 

Gauss proved that a regular polygon of n sides can be inscribed in a circle with Euclidean methods (e.g., by straightedge and compass) if and only if n is a power of two times a product of distinct Fermat primes.

 

Fibonacci sequence

Main article: Fibonacci sequence.

 

figurate number

A figurate number is a number sequence found by creating consecutive geometrical figures from arrangements of equally spaced points. Here is an example:

 

1	3	5	7
*	*	*	*
	**	*	*
		***	*
			****

 

The points can be arranged in one, two, three, or more dimensions. There are many different kinds of figurate numbers, such as polygonal numbers and tetrahedral numbers.

 

fraction

Main entry: fraction.

 

happy number

If you iterate the process of summing the squares of the decimal digits of a number and if this process terminates in 1, then the original number is called a happy number. For example 7 → (7²) 49 → (4² + 9²) 97 → (9² + 7²) 130 → (1² + 3²)10 → 1. See also amicable numbers.

 

Harshad number

A Harshad number is a number that is divisible by the sum of its own digits. For example, 1729 is a Harshad number because 1 + 7 + 2 + 9 = 19 and 1729 = 19 × 91. Harshad numbers are also known as Niven numbers.

 

A Harshad amicable pair is an amicable pair (m, n) such that both m and n are Harshad numbers. For example, 2620 and 2924 are a Harshad amicable pair because 2620 is divisible by 2 + 6 + 2 + 0 = 10 and 2924 is divisible by 2 + 9 + 2 + 4 = 17 (2924/17 = 172). There are 192 Harshad amicable pairs in first 5,000 amicable pairs.

 

hexadecimal

Hexadecimal is a number system in which each place has a value 16 times the value of the place at its right. Hexadecimal numbers are written using the symbols 0–9 and A–F (or a–f). The hexadecimal number 35B, for example, is equivalent to (3 × 256) + (5 × 16) + (11 × 1) = 859 in decimal.

 

Hexadecimal provides a convenient way to express binary numbers in modern computers in which a byte is almost always defined as containing eight binary digits. When showing the contents of computer storage – for example, when getting a core dump of storage in order to debug a new computer program or when expressing a string of text characters or a string of binary values – one hexadecimal digit can represent the arrangement of four binary digits. Two hexadecimal digits can represent eight binary digits, or a byte.

 

highest common factor

The highest common factor ff two or more integers is the largest integer which they share as a factor. For example, the highest common factor (hcf) of 15 and 17 is 1, since 17 is a prime number. In algebra, the hcf of two or more algebraic expressions may be found by examination of the factors of each: hence the hcf of 9ax² (= 3.3.a.a.x.x) and 3ax² (= 3.a.a.x) is 3a.x.

 

hyperfactorial

A hyperfactorial is a number such as 108, which is equal to 3³ × 2² × 1¹. In general, the n-th hyperfactorial H (n) is given by

 

H(n) = nⁿ (n – 1)^n–1 ... 3³ 2² 1¹

 

The first eight hyperfactorials are 1, 4, 108, 27648, 86400000, 4031078400000, 3319766398771200000, and 55696437941726556979200000.

 

See also large numbers and superfactorials.

 

hyperreal number

A hyperreal number is any of a colossal set of numbers, also known as nonstandard reals, that includes not only all the real numbers but also certain classes of infinitely large (see infinity) and infinitesimal numbers as well. Hyperreals emerged in the 1960s from the work of Abraham Robinson who showed how infinitely large and infinitesimal numbers can be rigorously defined and developed in what is called nonstandard analysis. Because hyperreals represent an extension of the real numbers, R, they are usually denoted by *R.

 

Hyperreals include all the reals (in the technical sense that they form an ordered field containing the reals as a subfield) and also contain infinitely many other numbers that are either infinitely large (numbers whose absolute value is greater than any positive real number) or infinitely small (numbers whose absolute value is less than any positive real number). No infinitely large number exists in the real number system and the only real infinitesimal is zero. But in the hyperreal system, it turns out that that each real number is surrounded by a cloud of hyperreals that are infinitely close to it; the cloud around zero consists of the infinitesimals themselves. Conversely, every (finite) hyperreal number x is infinitely close to exactly one real number, which is called its standard part, st(x). In other words, there exists one and only one real number st(x) such that x – st(x) is infinitesimal.

 

integer

An integer is any positive or negative whole number or zero: ...–3, –2, –1, 0, 1, 2, 3, ... "Integer" is Latin for "whole" or "intact." The set of all integers is denoted by Z, which stands for Zahlen (German for "number"). The integers are an extension of the natural numbers to include negative numbers and so make possible the solution of all equations of the form a + x = b, where a and b are natural numbers. Integers can be added and subtracted, multiplied, and compared. Like the natural numbers, the integers form a countably infinite set. However, the integers don't form a field since, for instance, there is no integer x such that 2x = 1; the smallest field containing the integers is that of the rational numbers. An important property of the integers is division with remainder: given two integers a and b with b not equal to 0, it is always possible to find integers q and r such that a = bq + r, and such that 0 ≤ r < |b|. q is called the quotient and r is called the remainder resulting from division of a by b. The numbers q and r are uniquely determined by a and b. From this follows the fundamental theorem of arithmetic, which states that integers can be written as products of prime numbers in an essentially unique way.

 

interesting numbers

Clearly some numbers are of greater interest (at least to mathematicians) than are others. The number pi, for instance, is far more interesting than 1.283 – or virtually any other number for that matter. Confining our attention to integers, can there be such a thing as an uninteresting number? It is easy to show that the answer must be "no." Suppose there were a set U of uninteresting integers. Then it must contain a least member, u. But the property of being the smallest uninteresting integer makes u interesting! As soon as u is removed from U, there is a new smallest uninteresting integer, which must then also be excluded. And so the argument could be continued until U was empty. Given that all integers are interesting can they be ranked from least to most interesting? Again, no. To be ranked as "least interesting" is an extremely interesting property, and thus leads to another logical contradiction!

 

When Srinivasa Ramanujan, the great Indian mathematician, was ill with tuberculosis in a London hospital, his colleague G. H. Hardy went to visit him. Hardy opened the conversation with: "I came here in taxi-cab number 1729. That number seems dull to me which I hope isn't a bad omen." Ramanujan replied, without hesitation: "Nonsense, the number isn't dull at all. It's quite interesting. It's the smallest number that can be expressed as the sum of two cubes in two different ways." (1729 = 1³ + 12³ and 9³ + 10³.)

 

irrational number

An irrational number is a real number that can't be written as one whole number divided by another; in other words, a real number that isn't a rational number. The decimal expansion of an irrational numbers doesn't come to an end or repeat itself (in equal length blocks), though it may have a pattern such as 0.101001000100001... The vast majority of real numbers are irrational, so that if you were to pick a single point on the real number line at random the chances are overwhelmingly high that it would be irrational. Put another way, whereas the set of all rationals is countable, the irrationals form an uncountable set and therefore represent a larger kind of infinity. Indeed, as the Harvard logician Willard Van Orman Quine pointed out: "The irrationals exist in such variety ... that no notation whatever is capable of providing a separate name for each of them."

 

There are two types of irrational number: algebraic numbers, such as the square root of 2, which are the roots of algebraic equations, and the transcendental numbers, such as π and e, which aren't. In some cases it isn't known if a number is irrational or not; undecided cases include 2^e, π^e, and the Euler-Mascheroni constant, γ (gamma).

 

An irrational number raised to a rational power can be rational; for instance, √2 to the power 2 is 2. Also, an irrational number to an irrational power can be rational. What kind of number is √2^√2? The answer is irrational. This follows from the so-called Gelfond-Schneider theorem, which says that if A and B are roots of polynomials, and A is not 0 or 1 and B is irrational, then AB must be irrational (in fact, transcendental).

 

Kaprekar number

Take a positive whole number n that has d number of digits. Take the square n and separate the result into two pieces: a right-hand piece that has d digits and a left-hand piece that has either d or d–1 digits. Add these two pieces together. If the result is n, then n is a Kaprekar number. Examples are 9 (9² = 81, 8 + 1 = 9), 45 (45² = 2025, 20 + 25 = 45), and 297 (297² = 88209, 88 + 209 = 297).

 

The first 20 Kaprekar numbers according to this definition are 1, 9, 45, 55, 99, 297, 703, 999, 2223, 2728, 4950, 5050, 7272, 7777, 9999, 17344, 22222, 77778, 82656, 95121, and 99999.

 

Kaprekar numbers can also be defined by higher powers. For example, 45³ = 91125, and 9 + 11 + 25 = 45. The first ten numbers with this property are: 1, 8, 10, 45, 297, 2322, 2728, 4445, 4544, and 4949. For fourth powers, the sequence begins 1, 7, 45, 55, 67, (100), 433, 4950, 5050, 38212, 65068. Notice that 45 is a Kaprekar number for second, third, and fourth powers (45⁴ = 4100625, and 4 + 10 + 06 + 25 = 45) – the only number in all three Kaprekar sequences, up to at least 400,000.

 

See also unique number.

 

Liouville number

A Liouville number is a transcendental number that can be approximated very closely by a rational number. Normally, proving that any given number is transcendental is difficult. However, the French mathematician Joseph Liouville (1809–1882) showed the existence of a large (in fact, infinitely large) class of transcendentals whose nature is easy to ascertain. A typical Liouville number is 0.101 001 000 000 100 000 000 000 000 000 000 000 01... in which the successive groups of zeros are of length 1!, 2!, 3!, 4!, and so on.

 

lowest common multiple

The lowest common multiple is the lowest number of which two or more positive whole numbers are factors. For example, the lowest common multiple of 2, 4, and 6 is 12.

 

lucky number

A lucky number is a number in a sequence, first identified and named around 1955 by Stanislaw Ulam, that evades a particular type of number "sieve" (similar to the famous Sieve of Eratosthenes), which works as follows. Start with a list of integers, including 1, and cross out every second number: 2, 4, 6, 8, ... The second surviving integer is 3. Cross out every third number not yet eliminated. This removes 5, 11, 17, 23, ... The third surviving number from the left is 7; cross out every seventh integer not yet eliminated: 19, 39, ... Repeat this process indefinitely and the numbers that survive are the "lucky" ones:

 

1 3 7 9 13 15 21 25 31 33 37 43 49 51 63 67 69 73 75 79 87 93 99 105 111 115 127 129 133 135 141 151 159 163 169 171 189 193 195 ...

 

Amazingly, though generated by a sieve based entirely on a number's position in an ordered list, the luckies share many properties with prime numbers. For example, there are 25 primes less than 100 and 23 luckies less than 100. In fact, it turns out that primes and luckies crop up about equally often within given ranges of integers. Also, the gaps between successive primes and the gaps between successive luckies widen at roughly the same rate as the numbers increase, and the number of twin primes – primes that differ by 2 – is close to the number of twin luckies. The luckies even have their own equivalent of the famous (still unsolved) Goldbach Conjecture, which states that every even number greater than 2 is the sum of two primes. In the case of luckies, it is conjectured that every even number is the sum of two luckies; no exception has yet been found. Another unresolved problem is whether there are an infinite number of lucky primes.

 

Mersenne number

A Mersenne number is a number of the form 2ⁿ – 1 (one less than a power of 2), where n is a positive integer. Mersenne numbers are named after Marin Mersenne who wrote about them in his Cogita Physica-Mathematica (1644) and wrongly conjectured that they were prime for n = 2, 3, 5, 7, 13, 17, 19, 31, 67, and 257, and composite for n > 257. See also Mersenne prime.

 

narcissistic number

A narcissistic number, also known as an Armstrong number or a plus perfect number, is an n-digit number equal to the sum of its digits raised to the nth power. For instance, 371 is narcissistic because 3³ + 7³ + 1³ = 371, and 9474 is narcissistic because 9⁴ + 4⁴ + 7⁴ + 4⁴ = 9474. The smallest narcissistic number of more than one digit is 153 = 1³ + 5³ + 3³. The largest narcissistic number (in base 10) is 115132219018763992565095597973971522401, which is the sum of the 39th powers of its digits. The reason there are no larger numbers is related to the fact that, as the number of digits increases, more and more 9's are required to get a sum that has n digits. For example, 10⁷⁰-1 is a number consisting of 70 nines in a row, and the sum of the 70th powers of its digits is 70 × 9⁷⁰ is approximately equal to 4.386051 × 10⁶⁸, which is only 69 digits long. So there is no way any 70-digit number can be equal to the sum of the 70th powers of its digits. The reason we see the last number occur at 39 digits is because, as the limit is approached, the number of big digits like 8's and 9's has to increase to make sure the sum will be big enough, but this means that there are a lot fewer combinations of digits to choose from.

 

natural number

A natural number is a number used for counting: 1, 2, 3, .... The debate about whether zero should also be included as a natural number has been going on for hundreds of years, and there's no general agreement even today. To avoid confusion, 0, 1, 2, 3, ..., are often referred to as non-negative integers or whole numbers, while 1, 2, 3, ..., are called positive integers.

 

Adding or multiplying natural numbers always produces other natural numbers. However, subtracting them can produce zero or negative integers, while dividing them produces rational numbers. An important property of the natural numbers is that they are well-ordered, in other words, every set of natural numbers has a smallest element. The deeper properties of the natural numbers, such as the distribution of prime numbers, are studied in number theory. Natural numbers can be used for two purposes: to describe the position of an element in an ordered sequence, which is generalized by the concept of ordinal number, and to specify the size of a finite set, which is generalized by the concept of cardinal number. In the finite world, these two concepts coincide; however, they differ when it comes to infinite sets (see infinity).

 

negative numbers

The introduction of the negative numbers is due to the need for subtraction to be performable without restriction. In the domain of positive numbers the subtraction a - b = c can only be carried out if a > b (a is greater than b). If, on the other hand, a < b (a is less than b) we define c = –(b – a), e.g., 5 – 7 = (–2). Here the "- sign" on the left hand side of the equation represents an operation; on the right hand side it forms part of the number itself. In the case of positive numbers the associated sign (+) may be omitted, but not in the case of negative numbers. Representation of the numbers on a straight line clarifies the notion of a negative number.

 

Long denied legitimacy in mathematics, negative numbers are nowhere to be found in the writings of the Babylonians, Greeks, or other ancient cultures. On the contrary, because Greek mathematics was grounded in geometry, and the concept of a negative distance is meaningless, negative numbers seemed to make no sense. They surface for the first time in in bookkeeping records seventh-century India and in a chapter of a work by the Hindu astronomer Brahmagupta. Their earliest documented use in Europe is in 1545 in the Ars magna of Girolamo Cardano. By the early 17th century, Renaissance mathematicians were explicitly using negative numbers but also meeting with heavy opposition. René Descartes called negative roots "false roots", and Blaise Pascal was convinced that numbers "less than zero" couldn't exist. Gottfried Leibniz admitted that they could lead to some absurd conclusions, but defended then as useful aids in calculation. By the eighteenth century, negative numbers had become an indispensable part of algebra.

 

Niven number

A Niven number is any whole number that is divisible by the sum of its digits. For example, 126 is a Niven number because, the sum of its digits 1 + 2 + 6, is 9, and 9 goes into 126 exactly 14 times. Niven numbers are name after the number theorist Ivan Niven who, in 1977, gave a talk at a conference in which he mentioned integers which are twice the sum of their digits. Then in a 1982 article, the mathematician Robert Kennedy christened numbers which are divisible by their digital sum in honor of Niven. They are also known as Harshad numbers.

 

normal number

A normal number is a number in which digit sequences of the same length occur with the same frequency. A constant is considered normal to base 10 if any single digit in its decimal expansion appears one-tenth of the time, any two-digit combination one-hundredth of the time, any three-digit combination one-thousandth of the time, and so on. In the case of pi, the digit 7 is expected to appear 1 million times among the first 10 million digits of its decimal expansion. It actually occurs 1,000,207 times – very close to the expected value. Each of the other digits also turns up with approximately the same frequency, showing no significant departure from predictions.

 

A number is said to be absolutely normal if its digits are normal not only to base 10 but also to every integer base greater than or equal to 2. In base 2, for example, the digits 1 and 0 would appear equally often.

 

Émile Borel introduced the concept of normal numbers in 1909 as a way to characterize the resemblance between the digits of a mathematical constant such as pi and a sequence of random numbers. He quickly established that there are lots of normal numbers, though finding a specific example of one proved to be a major challenge. The first to be found was Champernowne's Number, which is normal to base 10. Analogous normal numbers can be created for other bases.

 

To date, no specific "naturally occurring" real number has been proved to be absolutely normal, even though it is known that almost all real numbers are absolutely normal! However, in 2001, Greg Martin of the University of Toronto found some examples of the opposite extreme – real numbers that are normal to no base whatsoever.¹ To start with, he noted that every rational number is absolutely abnormal. For example, the fraction 1/7 can be written in decimal form as 0.1428571428571... The digits 142857 just repeat themselves. Indeed, an expansion of a rational number to any base b or b^k eventually repeats. Martin then focused on constructing a specific irrational absolutely abnormal number. He nominated the following candidate, expressed in decimal form, for the honor:

 

a = 0.6562499999956991999999...9999998528404201690728...

 

The middle portion (underlined) of the given fragment of a consists of 23,747,291,559 nines. Martin's formulation of this number and proof of its absolute abnormality involved so-called Liouville numbers.

 

1. G. Martin (2001). "Absolutely abnormal numbers". American Mathematical Monthly, 108, no. 8, 746–754.

 

numeral

A numeral is a symbol, or combination of symbols, that describes a number. Arabic numerals are the 10 digits from 0 to 9. Roman numerals, as normally used today, consist of seven letters or marks (I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, and M = 1,000). The formation of numbers from numerals depends on the number system used. See figure at the top of this page.

 

numerator

 

 

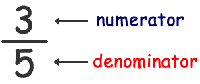The numerator is the number above the fraction bar that indicates the number of parts of the whole there are in a rational number. Below the fraction bar is the denominator.

 

oblong number

An oblong number is any number that is the product of two consecutive integers. Oblong numbers are also known as pronic numbers. The first few of them are: 0, 2, 6, 12, 20, and 30.

 

octonion

Octonions, also known as a Cayley numbers, are a non-associative generalization of the quaternions and the complex numbers involving numbers with one real coefficient and seven imaginary coefficients.

 

ordered pair

An ordered pair is a collection of two objects such that one can be distinguished as the first element and the other as the second element. An ordered pair with first element a and second element b is usually written as (a, b). Two such ordered pairs (a₁, b₁) and (a₂, b₂) are equal if and only if a₁ = a₂ and b₁ = b₂. Ordered triples and ordered n-tuples (ordered lists of n terms) are defined in the same way. An ordered triple (a, b, c) can be defined as (a , (b, c)), i.e. as two nested pairs.

 

ordinal number

An ordinal number is a number used to give the position in an ordered sequence: first, second, third, fourth ... Ordinal numbers are distinct from cardinal numbers (one, two, three, four, ...), which describe the size of a collection. The mathematician Georg Cantor showed in 1897 how to extend the concept of ordinals beyond the natural numbers to the infinite and how to do arithmetic with the resulting transfinite ordinals (see infinity).

 

palindromic number

A palindromic number is a number such as 1234321 that reads the same forwards and backwards; more generally, a symmetrical number written in some base a as a₁ a₂ a₃ ...|... a₃ a₂ a₁. In the familiar base 10 system, there are nine two-digit palindromic numbers: 11, 22, 33, 44, 55, 66, 77, 88, 99; there are 90 palindromics with three digits: 101, 111, 121, 131, 141, 151, 161, 171, 181, 191, ..., 909, 919, 929, 939, 949, 959, 969, 979, 989, 999; and there are 90 palindromics with four digits: 1001, 1111, 1221, 1331, 1441, 1551, 1661, 1771, 1881, 1991, ..., 9009, 9119, 9229, 9339, 9449, 9559, 9669, 9779, 9889, 9999, giving a total of 199 palindromic numbers below 10⁴. Below 10⁵ there are 1099 palindromics and for other exponents of 10ⁿ there are 1999, 10999, 19999, 109999, 199999, 1099999, ... It is conjectured, but has not been proved, that there are an infinite number of palindromic prime numbers.

 

With the exception of 11, palindromic primes must have an odd number of digits. A normally quick way to produce a palindromic number is to pick a positive integer of two or more digits, reverse the digits, and add to the original, then repeat this process with the new number, and so on. For example, 3462 gives the sequence 3462, 6105, 11121, 23232. Does the series formed by adding a number to its reverse always end in a palindrome? It used to be thought so. However, this conjecture has been proved false for bases 2, 4, 8, and other powers of 2, and seems to be false for base 10 as well. Among the first 100,000 numbers, 5,996 numbers are known that have not produced palindromic numbers by the add-and-reverse method in calculations carried out to date. The first few of these are 196, 887, 1675, 7436, 13783, 52514, ... A proof that these numbers never produce palindromes, however, has yet to be found. The largest known palindromic prime, containing 30,913 digits was found by David Broadhurst in 2003.

 

pandigital number

A pandigital number is an integer that contains each of the digits from 0 to 9 and whose leading digit is nonzero. The first few pandigital numbers are 1023456789, 1023456798, 1023456879, 1023456897, and 1023456978. A ten-digit pandigital number is always divisible by 9. If zeros are excluded, the first few "zeroless" pandigital numbers are 123456789, 123456798, 123456879, 123456897, 123456978, and 123456987, and the first few zeroless pandigital primes are 1123465789, 1123465879, 1123468597, 1123469587, and 1123478659. The sum of the first 32423 (a palindromic number) consecutive primes is 5897230146, which is pandigital. No other palindromic number shares this property. Examples of palindromic numbers that are the product of pandigital numbers are 2 970 408 257 528 040 792 (= 1 023 687 954 × 2 901 673 548) and 5 550 518 471 748 150 555 (= 1 023 746 895 × 5 421 768 309), both found in 2001. A pandigital product is a product in which the digits of the multiplicand, multiplier, and product, taken together, form a pandigital number.

 

partition number

A partition number is a number that gives the number of ways of placing n indistinguishable balls into n indistinguishable urns. For example:

 

1:   (*)
2:   (**) (*)(*)
3:   (***) (**)(*) (*)(*)(*)
5:   (****) (***)(*) (**)(**) (**)(*)(*) (*)(*)(*)(*)
7:   (*****) (****)(*) (***)(**) (***)(*)(*) (**)(**)(*) (**)(*)(*)(*) (*)(*)(*)(*)(*)
11: (******) (*****)(*) (****)(**) (****)(*)(*) (***)(***) (***)(**)(*) (***)(*)(*)(*) (**)(**)(**) (**)(**)(*)(*) (**)(*)(*)(*)(*) (*)(*)(*)(*)(*)(*)

 

The sequence runs: 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, ... If the urns are distinguishable, the number of ways is 2n. If the balls are distinguishable, the number of ways is given by the nth Bell number.

 

Pell numbers

Pell numbers are numbers that are similar to the Fibonacci numbers and are generated by the formula

 

A_n = 2A_n-1 + A_n-2.

 

The sequence runs: 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860, 33461, 80782, 195025, 470832, ... The ratio of successive terms approaches 1 plus the square root of 2.

 

perfect cube

A perfect cube is an integer of the form m ³ where m is an integer.

 

perfect number

A perfect number is a whole number that is equal to the sum of all its factors except itself. For example, 6 is a perfect number because its factors, 1, 2, and 3 add to give 6. The next smallest is 28 (the sum of 1 + 2 + 4 + 7 + 14). The ancient Christian scholar Augustine explained that God could have created the world in an instant but chose to do it in a perfect number of days, 6. Early Jewish commentators felt that the perfection of the universe was shown by the Moon's period of 28 days. The next in line are 496, 8128, and 33,550,336. As René Descartes pointed out: "Perfect numbers like perfect men are very rare." All end in 6 or 8, though what seems to be an alternating pattern of 6's and 8's for the first few perfect numbers doesn't continue. All are of the form 2^n-1(2ⁿ-1), where 2ⁿ-1 is a Mersenne prime, so that the search for perfect numbers is the search for Mersenne primes. The largest one known, as of Oct 2020, is 2^82,589,932(2^82,589,933 – 1). Written out in full it involves just under 50 million digits and starts and finishes as follows: 110847779864...007191207936. It isn't known if there are infinitely many perfect numbers or if there are any odd perfect numbers.

 

A pseudoperfect number or semi-perfect number is a number equal to the sum of some of its divisors, e.g. 12 = 2 + 4 + 6, 20 = 1 + 4 + 5 + 10. An irreducible semi-perfect number is a semi-perfect number, none of whose factors is semi-perfect, e.g. 104. A quasi-perfect number would be a number n whose divisors (excluding itself) sum to n + 1, but it isn't known if such a number exists. A multiply perfect number is a number n whose divisors sum to a multiple of n. An example is 120, whose divisors (including itself) sum to 360 = 3 × 120. If the divisors sum to 3n, n is called multiply perfect of order 3, or tri-perfect. Ordinary perfect numbers are multiply perfect of order 2. Multiply perfect numbers are known of order up to 8.

 

perfect power

A perfect power is an integer of the form mⁿ where m and n are integers and n > 1.

 

perfect square

A perfect square is a number that is the product of two equal whole numbers, e.g. 1 = 1 × 1, 4 = 2 × 2, 9 = 3 × 3, 16 = 4 × 4, 25 = 5 × 5.

 

polygonal number

A polygonal number is the number of equally spaced dots needed to draw a polygon. Polygonal numbers, which are a type of figurate number, include square numbers, triangular numbers, pentagonal numbers, and hexagonal numbers.

 

Polygonal numbers form an arithmetic sequence of the second order. The general term of these sequences is

z_n = n/2 [2 + (n - 1)d ],

where d is one of the numbers 1, 2, 3, ...

 

With d = 1 we obtain the triangular numbers: 1, 3, 6, 10, 15, ...

 

With d = 2 we obtain the square numbers: 1, 4, 9, 16, 25, ...

 

With d = 3 we obtain the pentagonal numbers: 1, 5, 12, 22, 35, ...

 

powerful number

A powerful number, also known as a squarefull number, is a positive whole number n such that for every prime number p dividing n, p ² also divides n. Every powerful number can be written as a ²b ³, where a and b are positive integers. The first 20 powerful numbers 1, 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 72, 81, 100, 108, 121, 125, 128, 144, and 169. There are pairs of consecutive powerful numbers, such as (8,9), (288,289), and (675,676). However, no three consecutive powerful numbers are known and, in 1978, Paul Erdös conjectured that none exist.

 

practical number

A practical number is a number n such that every positive integer less than n is either a divisor or a sum of distinct divisors of n. The first few practical numbers are 1, 2, 4, 6, 8, 12, 16, 18, 20, 24, ... All perfect numbers are practical.

 

prime number

Main article: prime number.

 

pronic number

A pronic number, also known as a rectangular or oblong number, is a number that is the product of two consecutive integers: 2 (1 × 2), 6 (2 × 3), 12 (3 × 4), 20 (4 × 5), ... The pronic numbers are twice the triangular numbers, and represent the lengths that produce the musical intervals: octave (1:2), fifth (2:3), fourth (3:4), major third (4:5) .... Pronic seems to be a misspelling of promic, from the Greek promekes, for rectangular or oblong; however, the "n" form goes back at least far as Leonhard Euler who used it in series one, volume fifteen of his Opera.

 

pyramidal number

A pyramidal number is the number of dots that may be arranged in a pyramid with a regular polygon as base.

 

Pythagorean triplet

A Pythagorean triplet, also called a Pythagorean triple, is a set of three whole numbers that satisfies Pythagoras's theorem, i.e. the squares of two of the numbers add up to the square of the third number. Examples include (3, 4, 5), (5, 12, 13), and (7, 24, 25). These are called primitive triplets because they have no common divisors. If the members of a primitive triplet are multiplied by the same integer the result is a new (but not primitive) triplet.

 

In any primitive Pythagorean triplet, one, and only one, of the three numbers must be even (but can't equal 2); the other two numbers are relatively prime. There are infinitely many such triplets, and they are easy to generate using a classic formula, known since ancient times. If the numbers in the triplet are a, b, and c, then: a = n ² – m ², b = 2mn, c = m ² + n ², where m and n are two integers and m is less than n. Because the square root of two is irrational, there can't be any Pythagorean triplets (a, a, c). However, there are an infinite number of triplets (a, a + 1, c), the first three of which (apart from the trivial (0, 1, 1)) are (3, 4, 5), (20, 21, 29), and (119, 120, 169). There are also an infinite number of Pythagorean quartets (a, b, c, d) such that a ² + b ² + c ² = d ². This is simply the three-dimensional form of Pythagoras's theorem and can be interpreted as the fact that the point in three-dimensions with Cartesian coordinates (a, b, c) lies an integer distance d from the origin.

 

A formula that generates Pythagorean quartets is: a = m ², b = 2mn, c = 2n ²; d = (m ² + 2n ²) = a + c. Also note that b ² = 2ac. When m = 1 and n = 1, we get the quarter (1, 2, 2, 3) – the simplest example. Although there are an infinite number of Pythagorean triplets, Fermat's last theorem, which is now know to be true, ensures that there are no triplets for higher powers.

 

See also Euler's conjecture and multigrade.

 

quaternion

 

Irish stamp commemorating the discovery of quaternions by William Hamilton

 

A quaternion is an ordered set of four numbers. Quaternions, first introduced by William Hamilton, can also be written in the form a + bi + cj + dk, where a, b, c, and d are real numbers and i, j, and k are imaginary numbers defined by the equations i ² = j ² = k ² = –1 and –ji = k. Quaternions are similar to complex numbers, but whereas complex numbers can be represented by points of a two-dimensional plane, quaternions can be viewed as points in four-dimensional space (see fourth dimension).

 

For a while, quaternions were very influential: they were taught in many mathematics departments in the United States in the late 1800s, and were a mandatory topic of study at Dublin, where Hamilton ran the observatory. William Clifford developed the theory of them further. But then they were driven out by the vector notation of William Gibbs and Oliver Heaviside. Had quaternions come along later, when theoretical physicists were trying to understand patterns among subatomic particles, they may have found a place in modern science; after all, the unit quaternions form the group SU(2), which is perfect for studying spin-½ particles. But the way things turned out, quaternions had fallen from favor by the 20th century and Wolfgang Pauli used 2 × 2 complex matrices instead to describe the generators of SU(2).

 

rational number

A rational number is a number that can be written as an ordinary fraction – a ratio, a/b, of two integers, a and b, where b isn't zero – or as a decimal expansion that either stops (like 4.58) or is periodic (like 1.315315...). Other examples include 1, 1.2, 385.66, and 1/3.

 

Rational numbers are countable, which means that, although there are infinitely many of them, they can always be put in a definite order, from smallest to largest, and can thus be counted. They also form what's called a densely ordered set; in other words, between any two rationals there always sits another one – in fact infinitely many other ones.

 

The rational numbers are a subset of the real numbers; real numbers that aren't rational are called, rationally enough, irrational numbers. Although rationals are dense on the real number line, in the sense that any open set contains a rational, they're pretty sparse in comparison with the irrationals. One way to think of this is that the infinity of rationals (which, strangely enough, is exactly the same size as the infinity of whole numbers) is smaller than the infinity of irrational numbers. Another way to grasp the scarcity versus density issue, is to realize that the rationals can be covered by a set whose "length" is arbitrarily small. In other words, given a string of any positive length, no matter how short, it will still be long enough to cover all the rationals. In mathematical parlance, the rationals are a measure zero set. The irrationals, by contrast, are a measure one set. This difference in measure means that the rationals and irrationals are quite different even though a rational can always be found between any two irrationals, and an irrational exists between any two rationals.

 

For more, see the separate article on rational numbers.

 

real number

A real number is any number that can be represented as a, possibly infinitely long and non-repeating, decimal. Real numbers stand in one-to-one correspondence with the points on a continuous line, known as the real number line, that stretches from zero to infinity in both directions. The set of real numbers contains the set of all rational numbers and the set of all irrational numbers. The name "real number" is a retronym, coined by René Descartes in response to the concept of imaginary numbers. Number systems that are even more general that the real numbers include the complex numbers and, of much more recent discovery, hyperreal numbers and surreal numbers.

 

rectangular number

Arectangular number is a number that can be represented in the shape of a rectangle, for example, 6 (2 × 3) and 15 (3 × 5). More generally, a rectangular number can be written in the form m × n, where m and n are positive integers greater than 1. If m = n, then the number is also a square number.

 

 

relatively prime

Two integers are relatively prime if they share no common positive factors (divisors) except 1. For example, 12 and 13 are relatively prime, but 12 and 14 are not.

 

repdigit

A repdigit is a number composed of repetition of a single digit in a given base, generally taken as base 10 unless otherwise specified. For example, the Beast Number 666 is a (base-10) repdigit.

 

rep-unit

A rep-unit is a number whose digits are all units; the rep-unit (repeated unit) with n digits is denoted R_n. For example, R₁ = 1, R₂ = 11, R₃ = 111, and R_n = (10ⁿ – 1)/9. R_n divides R_m whenever n divides m. No repunit can be a square number, but it is not known if one can be a cube. Repunit primes are repunits that are prime numbers. The only known repunit primes are R₂ (11), R₂₃, R₁₉, R₃₁₇, and R₁₀₃₁, though R₄₉₀₈₁ and R₈₆₄₅₃ are suspected primes.

 

Roman numerals

Roman numerals are a number system in which each symbol represents a fixed value regardless of its position; this differs from the place-value system of Arabic numerals. The earliest form of the Roman system was, however, decimal. In this primitive version a series of I's represented any number from 1 to 9, and a new symbol was introduced for each higher power of 10: X for 10, C for 100, and M for 1,000. The symbols V, L, and D, which stand for 5, 50, and 500, are thought to have been introduced by the Etruscans. For example, VIII is 8, XL is 40, MCD is 1400, and MCDXLVIII is 1448.

 

A common remark is that multiplication and division using Roman numerals is so awkward as to be totally impractical. However, an article by James G. Kennedy in The American Mathematical Monthly in 1980 gives algorithms for these operations that are actually more straightforward in the Roman system than in the Arabic. In multiplication the first step is to rewrite the numbers in a simple place-value notation. Seven columns are set up, headed by the symbols M, D, C, L, X, V, and I, and tallies are marked in each column corresponding to the number of times that symbol appears in the multicand. For example, if the multiplicand is XIII (13), one tally is marked in the X column and three tallies are marked in the I column. The multiplier is written in the same way. The multiplication itself is done by forming partial products according to two simple rules. In most cases the partial product given by any one tally in the multiplier is simply the set of tallies that represents the multiplicand, shifted to the left an appropriate number of columns. If the multiplier digit is I, the multiplicand is not shifted at all; the multiplicand is shifted one place to the left for V, two places for X, three places for L, and so on. The second rule is applied only when one Etruscan character is multiplied by another. In such cases the tallies representing the multiplicand digit are written twice in the appropriately shifted column and an additional tally is written one column to the right. Once a partial product has been formed for every tally in the multiplier, the tallies in each column are accumulated and replaced by the Roman symbol at the head of the column, giving the final answer. Only a slight change in the method is needed for Roman numerals in "subtractive notation," where 10 is written as IX, and so on. If all this sounds not quite so simple, the method for multiplying Arabic numbers is just as involved if they are written in explicit form. Furthermore, Arabic operations require a multiplication table giving the 100 products of all the possible pairs of Arabic digits. No comparable table is needed with Roman numerals, where all arithmetical operations can be defined in terms of shifting rules, addition, and subtraction.

 

sexagesimal

Sexagesimal is of, relating to, or based upon the number sixty. Sexagesimal refers especially to the number system with base 60. The Babylonians began using such a scheme around the beginning of the second millennium BC. in what was the first example of a place-value system. Our degree of 60 minutes, minute of 60 seconds (in both time and angle measure), and hour of 60 minutes hark back to this ancient method of numeration. Quite why the Babylonians counted using sexagesimal isn't known, but 60 certainly has more factors than any other number of comparable size.

 

Sierpinski number

A Sierpinski number is a positive, odd integer k such that k times 2ⁿ + 1 is never a prime number for any value of n. In 1960 Waclaw Sierpinski showed that there were infinitely many such numbers (though he didn't give a specific example.) This a strange result. Why should it be that while the vast majority of expressions of the form m times 2ⁿ + 1 eventually produce a prime, some don't? For now, mathematicians are focused on a more manageable problem posed by Sierpinski: What is the smallest Sierpinski number? In 1962, John Selfridge discovered what is still the smallest known Sierpinski number, k = 78557. The next largest is 271129. Is there a smaller Sierpinski number? No one yet knows. However, to establish that 78557 is really the smallest, it would be sufficient to find a prime of the form k(2ⁿ + 1) for every value of k less than 78557. In early 2001, there were only 17 candidate values of k left to check: 4847, 5359, 10223, 19249, 21181, 22699, 24737, 27653, 28433, 33661, 44131, 46157, 54767, 55459, 65567, 67607, and 69109. In March 2002, Louis Helm of the University of Michigan and David Norris of the University of Illinois started a project called "Seventeen or Bust," the goal of which is to harness the computing power of a worldwide network of hundreds of personal computers to check for primes among the remaining candidates. The team's effort have so far eliminated five candidates – 46157, 65567, 44131, 69109, and 54767. Despite this encouraging start, it may take as long as a decade, with many additional participants, to check the dozen remaining candidates.

 

Smith number

A Smith number is a composite number, the sum of whose digits equals the sum of the digits of its prime factors. The name stems from a phone call in 1984 by the mathematician Albert Wilansky to his brother-in-law, called Smith, during which Wilansky noticed that the phone number, 4937775, obeyed the condition just mentioned. Specifically:

 

4937775 = 3 × 5 × 5 × 65837

 

Trivially, all prime numbers have this property, so they are excluded. The Smith numbers less than 1000 are:

4, 22, 27, 58, 85, 94, 121, 166, 202, 265, 274, 319, 346, 355, 378, 382, 391, 438, 454, 483, 517, 526, 535, 562, 576, 588, 627, 634, 636, 645, 648, 654, 663, 666, 690, 706, 728, 729, 762, 778, 825, 852, 861, 895, 913, 915, 922, 958, and 985.

In 1987, Wayne McDaniel proved that there are infinitely many Smiths.

 

square free

A square free number is an integer that is not divisible by a perfect square, n ², for n > 1.

 

square number

A square number is a number that is the product of two equal integers, e.g. 49 is a square number because 49 = 7 × 7. Square numbers are a type of polygonal number (Fig 2).

 

standard form

Standard form is a scientific method of writing numbers, especially very large or very small numbers. The first non-zero digit of the number is placed before the decimal point and all other digits are placed in order after the decimal point. This decimal is multiplied by an appropriate power of 10. For example, 1,721,448 is written as 1.721 448 × 10⁶ in standard form and 0.003378159 is written as 3.378 159 × 10^–3.

 

sublime number

A sublime number is a number such that both the sum of its divisors and the number of its divisors are perfect numbers. The smallest sublime number is 12. There are 6 divisors of 12 – 1, 2, 3, 4, 6, and 12 – the sum of which is 28. Both 6 and 28 are perfect. The second sublime number begins 60865..., ends ...91264, and has a total of 76 digits! It is not known if there are larger even sublime numbers, nor if there are any odd sublime numbers.

 

superfactorial

A superfactorial is the product of the first n factorials (definition by Neil Sloane and Simon Plouffe in 1995). For example:

 

sf(4) = 1! × 2! × 3! × 4! = 288

 

The sequence of superfactorials starts (from n = 0) as

 

1, 1, 2, 12, 288, 34560, 24883200, ...

 

This idea was extended in 2000 by Henry Bottomley to the superduperfactorial as the product of the first n superfactorials, starting (from n = 0) as

 

1, 1, 2, 24, 6912, 238878720, 5944066965504000, ...

 

surd

A surd is a little-used term meaning the square root of a whole number that has an irrational value. Some examples are √2 (see square root of 2), √3, and √10.

 

A surd can often be simplified using the fact that √(ab) = √a × √b. For example, √12 = √(4 × 3) = √4 × √3 = 2√3.

 

Surds may be used to express some results in exact form, such as sin 60° = √3/2.

 

surreal number

A surreal number is a member of a mind-bogglingly vast class of numbers that includes all of the real numbers, all of Georg Cantor's infinite ordinal numbers (different kinds of infinity), a set of infinitesimals (infinitely small numbers) produced from these ordinals, and strange numbers that previously lived outside the known realm of mathematics. Each real number, it turns out, is surrounded by a "cloud" of surreals that lie closer to it than do any other real number. One of these surreal clouds occupies the curious space between zero and the smallest real number greater than zero and is made up of the infinitesimals.

 

Surreal numbers were invented or discovered (depending on your philosophy) by John Conway to help with his analysis of certain kinds of games. The idea came to him after watching the British Go champion playing in the mathematics department at Cambridge. Conway noticed that endgames in Go tend to break up into a sum of games, and that some positions behaved like numbers. He then found that, in the case of infinite games, some positions behaved like a new kind of number – the surreals. The name "surreal" was introduced by Donald Knuth in his 1974 book Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness.¹ This novelette is notable as being the only instance where a major mathematical idea has been first presented in a work of fiction. Conway went on to describe the surreal numbers and their use in analyzing games in his 1976 book On Numbers and Games.² The surreals are similar to the hyperreal numbers, but they are constructed in a very different way and the class of surreals is larger and contains the hyperreals as a subset.

 

1. Knuth, Donald. Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness. Reading, Mass.: Addison-Wesley, 1974.
2. Conway, John Horton. On Numbers and Games. New York: Academic Press, 1976.

 

tetrahedral number

A tetrahedral number is a number that can be made by considering a tetrahedral pattern of beads in three dimensions. For example, if a triangle of beads is made with three beads to a side, and on top of this is placed a triangle with two beads to a side, and on top of that a triangle with one bead to a side, the result is a tetrahedron of beads. In this case the total number of beads is (3rd triangular number) + (2nd triangular number) + (1st triangular number) = 6 + 3 + 1 = 10. In general the nth tetrahedral number is equal to the sum of the first n triangular numbers. This is the same as the 4th number from the left in the (n + 3)th row of Pascal's triangle. We can use the binomial formula for numbers in Pascal's triangle to show that the nth tetrahedral number is ⁿ⁺²C₃, or (n + 2)(n + 1)n/6. The only numbers that are both tetrahedral and square are 4 (= 2² = T₂) and 19600 (= 140² = T₄₈).

 

transcendental number

A transcendental number is a number that can't be expressed as the root of a polynomial equation with integer coefficients. Transcendental numbers are one of the two types of irrational number, the other being algebraic numbers. Their existence was proved in 1844 by the French mathematician Joseph Liouville (1809–1882). Georg Cantor showed (1874) that there are more transcendental than algebraic numbers; the set of all algebraic numbers is enumerable (like the integers); the set of transcendental numbers is not.

 

Although transcendentals make up the vast majority of real numbers, it is often surprisingly hard, and may even be impossible, to tell whether a certain number is transcendental or algebraic. For example it is known that both π and e are transcendental and also that at least one of π + e and π × e must be transcendental, but it is not known which. It is also known that e ^π is transcendental. This follows from the Gelfond-Schneider theorem, which says that if a and b are algebraic, a is not 0 or 1, and b is not rational, then a ^b is transcendental. Using Euler's formula, e ^{i π} = –1, and taking both sides to the power –i gives (–1)^–i = (e^{i π})^–i = e ^π. Since the theorem tells us that the left hand side is transcendental, it follows that the right hand side is too. (It also follows that e × π and e + π are not both algebraic, because if they were then the equation x ² + x(e + π) + eπ = 0 would have roots e and π, making both numbers algebraic.) But although it is known that e^π is transcendental, the status of e ^e, π ^e, and π ^π remains uncertain.

 

transfinite number

A transfinite number is any of the infinite ordinal numbers first described by Georg Cantor.

 

triangular number

 

 

A triangular number is any number that can be represented by a triangular array of dots. 1, 3, 6, 10, ... are triangular numbers. The nth triangular number is n(n + 1)/2. Every integer is the sum of at most three triangular numbers. Every even triangular number is a perfect number. If T is a triangular number, 8T + 1 is a perfect square and 9T + 1 is another triangular number. The square of the nth triangular number is equal to the sum of the first n cubes. Certain triangular numbers are also squares, but no triangular number can be a third, fourth or fifth power, nor can one end in 2, 4, 7, or 9.

 

undulating number

An undulating number is an integer whose digits, in a given base, alternate – that is, one written in the form ababab..., where a and b are digits. For example, 434343 and 101010101 are undulating numbers.

 

unique number

A unique is the constant U_n that results if a number A_n consisting of n consecutive digits, in ascending order, is subtracted from the number A_n' obtained by reversing the digits of A_n. For example, a three-digit number 345, if subtracted from its reverse 543, yields a difference of 198. Any other three-digit number subtracted from its reverse gives the same difference. Thus U₃ = 198. Similarly for a number with four consecutive digits, the unique number U₄ = 3087. The first ten unique numbers are: U₁ = 0, U₂ = 9, U₃ = 198, U₄ = 3087, U₅ = 41976, U₆ = 530865, U₇ = 6419754, U₈ = 75308643, U₉ = 864197532, and U₁₀ = 9753086421. Unique numbers are related to Kaprekar numbers, K_n, by the formula

 

U_n + U_n' = K_n + K_n'.

 

For example, when n = 4, K₄ = 6174, K₄' = 4716, U₄ = 3087, U₄' = 7803, and

3087 + 7803 = 10890 = 6174 + 4716.

 

1. Gupta, S. S. "Unique Numbers", Science Today, January 1988, India.

 

unit fraction

A unit fractionis the fraction whose numerator (number on top) is 1.

 

untouchable number

A untouchable number is any number that is not the sum of the aliquot parts of any other number. The first few untouchable numbers are 2, 5, 52, and 88.

 

vampire number

A vampire number is a natural number x that can be factorized as y × z in such a way that the number of occurrences of a particular digit in the representation of x in a given base (say 10) appears the same number of times in the representations in that same base of y and z together. For example, 2187 is a vampire number since 2187 = 81 × 27 ; similarly 136948 is a vampire because 136948 = 146 × 938. Vampire numbers are a whimsical idea that was introduced by Clifford Pickover in 1995. ¹

 

1. Pickover, Clifford. Keys to Infinity. New York: W. H. Freeman, 1995.

 

vigesimal

Vigesimal means, relating to, or based on the number 20; the term comes from the Latin vigesimus for "twentieth." Mayan arithmetic, which took account of all the toes as well as the fingers, used a vigesimal system. In place of the multiples of 10 used in the decimal system, 1, 10, 100, 1000, 10000, ..., the Mayans dealt in multiples of 20: 1, 20, 400, 8000, 160000, ...

 

winding number

A winding number is the number of times a closed curve in the plane passes around a given point in the counterclockwise direction.