Pythagoras' theorem
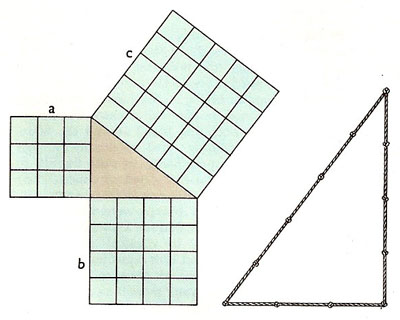
Above left. Pythagoras' theorem demonstrated in the case of the 3, 5, 5 triangle (one having sides in the ratio 3:4:5). It can be seen by inspection that in this case a2 + b 2 = c 2. Other right-angled triangles, the ratios of whose sides can be expressed using only small integers are 5, 12, 13 and 8, 15, 17 triangles. Above right: The ancient method of laying out a right angle using a knotted rope was known and used long before the time of Pythagoras.
Pythagoras' theorem states that the square of the length of the hypotenuse (the longest side) of a right triangle is the sum of the squares of the lengths of the other two sides. This is usually expressed as a 2 + b 2 = c 2.
Even though there are ancient Babylonian tablets that express the Pythagorean theorem in terms of the measurements found in right triangles the Greek mathematician Pythagoras of Samos is widely credited with identifying the equation. No original works by Pythagoras remain to prove this definitely though, and it is impossible to determine if the idea was his alone. However, it is claimed that upon discovering his eponymous mathematical truth, Pythagoras offered a hetacomb to the gods (a public sacrifice of 100 oxen). He and many of his contemporaries believed that mathematics was so connected to the divine that they formed a religious movement around this discovery. However, when he and his followers – who dubbed themselves the Brotherhood of Pythagoreans – moved to Croton, a Greek colony in southern Italy, their controversial beliefs led to public outcry, forcing them to flee for their lives.
The Pythagorean theorem is not merely a deduction about right triangles and the relationship of their sides. It has since become a foundational mathematical theorem, and an indelible part of the modern world. Through it, Pythagoras showed that te abstract notions of numbers and mathematics correspond to humanity's everyday perceptions of the real world. His theorem revealed that nature had a structure, a structure composed of equations, and those equations were something humanity could comprehend, measure, and use.

