A triangle is a three-sided polygon. The sum of the interior angles of a triangle is always 180°, unless the triangle is drawn in a non-Euclidean geometry . Triangles can be classified either by their angles, as acute, obtuse, or right; or by their sides, as scalene (all different), isosceles (two the same), or equilateral (all equal).

 

A right triangle (or right-angled triangle) has one interior angle equal to 90°, and may be either scalene or isosceles. The hypotenuse is the longest side of a right triangle – the one opposite the right angle. The word comes from the Greek roots hypo meaning 'under' (which also appears, for example, in 'hypodermic' – 'under the skin') and tein or ten, for 'stretch'. Thus the hypotenuse is the line segment 'stretched under' the right angle. See also Pythagoras' theorem.

 

Various formulae link the dimensions of a triangle (see diagram). The cosine formula states that a ² = b ² + c ² - 2bc cos A, and the sine formula that a / sin A = b / sin B = c / sin C. If s = 1/2 (a + b + c), the area of the triangle is √[s(s – a)(s – b)(s – c)].

 

Other types of triangle

A Pythagorean triangle is a right triangle whose sides all have integer lengths. A primitive Pythagorean triangle is one whose sides are relatively prime.

 

A medial triangle is a triangle whose vertices are the midpoints of the sides of a given triangle. An orthic triangle is a triangle whose vertices are the feet of the altitudes of a given triangle.

 

A limping triangle is right triangle whose two shorter sides (i.e., those other than the hypotenuse) differ in length by one unit. An example is the 20–21–29 triangle (20² + 21² = 29²).

 

The pedal triangle of a point P with respect to a triangle ABC is the triangle whose vertices are the feet of the perpendiculars dropped from P to the sides of triangle ABC.

 

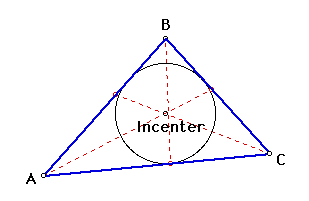
Incenter

The incenter is the point of concurrence of the lines drawn bisecting the angles of a triangle. As this point is equidistant from the sides, it is the center of the circle that may be inscribed in the triangle.

 

 

Triangular Lodge

 

 

The Triangular Lodge is one of the few triangular buildings in England. It was built by Sir Thomas Tresham in about 1595 at Rushton, Northamptonshire. Tresham was a Catholic (spending some 15 years in prison because of this) and also a mystic numerologist. The whole design of the Lodge is based on the number three, which Tresham saw connected with his own surname and as an expression of his faith in the Christian Trinity. The Lodge's ground plan is a perfect equilateral triangle, each side 33 feet long – by tradition, the age of Christ at his death. The building has three floors, each floor has three windows, and each window is a three-fold trefoil. There are three gables and three gargoyles on each side. Even the central chimney is three-sided. The inscriptions all have 33 letters. Other buildings with a three-sided equilateral theme in Europe include a triangular castle at Gripsholm in Sweden and part of the Chateau de Chantilly in France, which is based on an equilateral plan of gigantic scale.