polygon
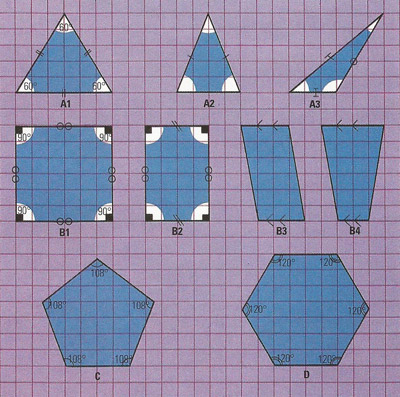
Figure 1. Polygons are many-sided plane figures, the sides and angles of which may be equal or unequal, giving symmetrical or asymmetrical shapes. The simplest figure is the equilateral triangle (A1) which has all sides and angles equal. The isosceles triangle (A2) has two sides equal while (A3), which happens to be obtuse, has sides of differing length. The simplest quadrilateral (B1) is the square with equal sides and equal internal angles. The rectangle (B2) has two pairs of equal and opposite sides with equal internal angles. The parallelogram (B3) has two pairs of equal and opposite parallel sides. The trapezium (B4) has only two parallel sides. The regular pentagon (C) has five equal sides and the regular hexagon (D), six.
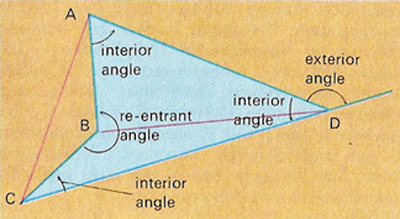
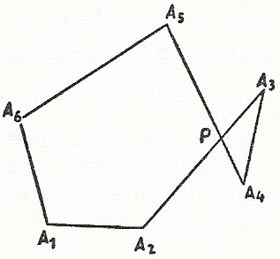
Figure 2. The polygon ABCD is an irregular quadrilateral with acute angles at A, C, and D and a reentrant angle at B. AC and BD are its diagonals.
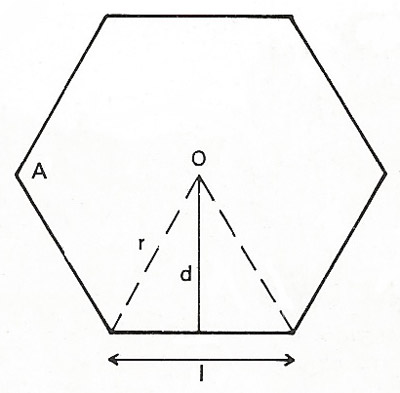
Figure 3. A regular polygon.
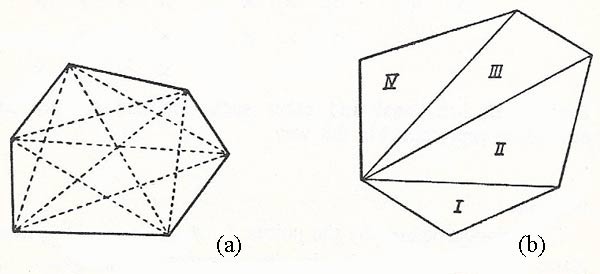
Figure 4. Polygon diagonals and triangles.
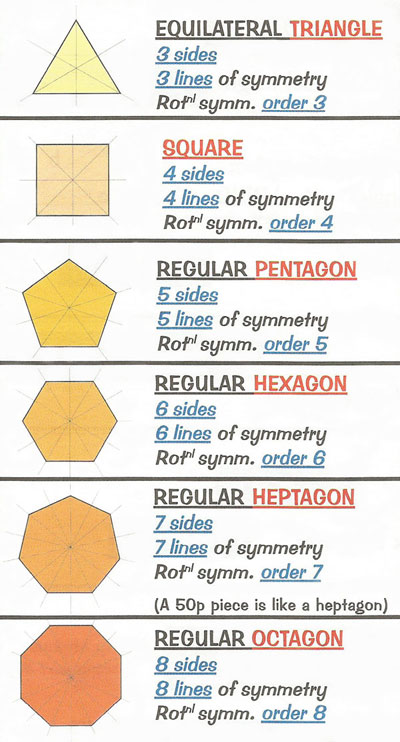
Figure 5. Regular polygons named.
A polygon is a plane closed figure whose sides are straight lines. The term polygon (from the Greek poly for 'many' and gwnos for 'angle') sometimes also refers to the interior of the polygon (the open area that this path encloses) or to the union of both.
A polygon is simple if it is described by a single, non-intersecting boundary. In this case, the vertices A1, A2, A3, ..., An, are all different, and two segments have no point in common unless they are adjacent segments, in which case they have a vertex in common. The figure below, however, shows a polygon that does not satisfy these conditions and is known as a complex polygon
 |
A simple polygon is called convex if it has no internal angles greater than 180° otherwise it is called concave. A polygon is called regular if all its sides are of equal length and all its angles are equal (Figure 3).
| Regular polygons | ||
|---|---|---|
| name | sides | interior angle = 180° - (360°/sides) |
| equilateral triangle | 3 | 60° |
| square | 4 | 90° |
| regular pentagon | 5 | 108° |
| regular hexagon | 6 | 120° |
| regular heptagon | 7 | 128.57° (approx.) |
| regular octagon | 8 | 135° |
| regular nonagon | 9 | 140° |
| regular decagon | 10 | 144° |
| regular hectagon | 100 | 176.4° |
| regular megagon | 106 | 179.99964° |
| regular googolgon | 10100 | 180° (approx.) |
Any polygon, regular or irregular, has as many angles as it has sides. Every n-sided polygon has n(n – 3)/2 diagonals. A diagonal is a segment joining two vertices which are not sides of the polygon, so that from each vertex proceed two sides and (n – 3) diagonals (Figure 4a). Every n-sided polygon can be divided into (n – 2) triangles (Figure 4b).
An n-gon is a polygon with n sides. For example, a hexagon is a 6-gon.
A self-intersecting polygon is a polygon with edges that cross other edges.
Formulae for regular polygons
In a regular n-sided polygon (Figure 3), angle A = 180(1 – 2/n); angle O = 360/n; the area of the polygon = 1/2nld; and the radius r = d.sec(180/n).
Types of polygon
Pentagon
A pentagon is a five-sided polygon; its interior angles add up to 540° and are each 108° in the case of a regular polygon.
Hexagon
A hexagon is a six-sided polygon.
Heptagon
 |
A heptagon is a polygon with seven sides. The sum of the interior angles of a polygon is 900°. In the case of a regular heptagon, each interior angle is approximately 128.57°. The area of a regular heptagon of side length a is (7/4)a2 cot (π/7).
Octagon
 |
An octagon is an 8-sided polygon. The sum of the interior angles of an octagon is 1080 degrees. A regular octagon – one in which all the sides and all the angles are equal – is constructible with a compass and straightedge.
Nonagon
 |
A nonagon is a polygon with 9 sides. The sum of the interior angles of a nonagon is 1260° A nonagonal number is a number of the form n(7n – 5)/2.
Decagon
 |
A decagon is a polygon with 10 sides. Each interior angle of a regular decagon is 144°.
Cyclic polygon
A cyclic polygon is a polygon with vertices that all lie on the same circle. All triangles are cyclic (but not all of any other kind of polygon) because any set of three points, not lying on a single line, can have a circle drawn through it.
Vertex figure
The vertex figure is the polygon that appears if a polyhedron is truncated at a vertex. The vertex figure of a cube, for example, is an equilateral triangle. To ensure consistency, the truncation may be done at the midpoints of the edges.


