square root of 2
The square root of 2 has the approximate value 1.41421356 ...
It was the first number shown to be what is now known as an irrational number (a number that can't be written in the form a/b, where both a and b are integers.) This discovery was made by Pythagoras or, at any rate, by the Pythagorean group that he founded.
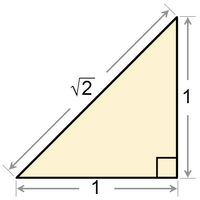
The square root of 2 is the length of the hypotenuse (longest side) of a right triangle whose other two sides are each one unit long. A reductio ad absurdum proof that √2 is irrational is straightforward. Suppose that √2 is rational, in other words that √2 = a/b, where a and b are coprime integers (that is, they have no common factors other than 1) and b > 0. It follows that a 2/b 2 = 2, so that a 2 = 2b 2. Since a 2 is even (because it has a factor of 2), a must be even, so that a = 2c, say. Therefore, (2c)2 = 2b 2, or 2c 2 = b 2, so b must also be even. Thus, in a/b, both a and b are even. But we started out by assuming that we'd reduced the fraction to its lowest terms. So there is a contradiction and therefore √2 must not be irrational. This type of proof can be generalized to show that any root of any natural number is either a natural number or irrational.
As a continued fraction, √2 can be written 1 + 1/(2 + 1/(2 + 1/(2 + ... ))), which yields the series of rational approximations: 1/1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, ... Multiplying each numerator (number on the top) by its denominator (number on the bottom) gives the series 1, 6, 35, 204, 1189, 6930, 40391, 235416, ... which follows the pattern: An = 6An-1 - An–2. Squaring each of these numbers gives 1, 36, 1225, 41616, 1413721, 48024900, 1631432881, ..., each of which is also a triangular number. The numbers in this sequence are the only numbers that are both square and triangular.

