Leonhard Euler was a great Swiss mathematician, the second most prolific mathematician in history (in terms of publications), after Paul Erdös. His greatest contributions were to number theory, but Euler also did important work in calculus, geometry, algebra, probability, acoustics, optics, mechanics, astronomy, artillery, navigation, and finance. He had a knack of coming up with important results by intuition, he cast calculus and trigonometry in their modern forms, and he showed the importance of the number e. Even the amusing puzzles he invented and, in some cases, solved have opened up new mathematical fields. The Bridges of Königsberg problem, for example, heralded the beginning of graph theory and topology, while his Thirty-six Officers Problem stimulated important work in combinatorics. Euler also worked on magic squares and the problem of the knight's tour.

Along with Joseph Lagrange, Pierre Laplace, and others, Euler helped develop the science of celestial mechanics. He applied powerful new mathematical techniques to problems of cometary orbits, planetary perturbations, and the tides. He also refined the theory of the Moon's motion and calculated more accurate orbits for Jupiter and Saturn.

 

Having learned some math from his father, a Calvinist preacher, Euler studied at the University of Basle where he became close friends with members of the Bernoulli family. In 1727, he moved to St. Petersburg, to the court of Catherine the Great, becoming professor of physics (1730) and of mathematics (1733). A devout Christian, Euler met in Russia the encyclopedist and philosopher René Diderot, a notorious atheist. When Diderot heard that Euler had a mathematical proof of the existence of God, he asked for it and was quoted the equation now often referred to as Euler's identity. Upon losing the use of his right eye, Euler said "Now I will have less distraction." Indeed, the quantity of his output seemed to be inversely proportional to the quality of his sight, because his rate of publication increased after he became almost totally blind in 1766. Euler died moments after calculating the orbit of Uranus on 18 September 1783.

 

Major ideas and results named after Euler

 

Euler's identity

 

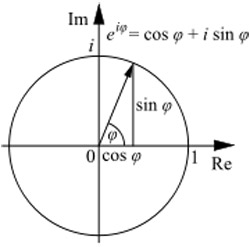
Euler's formula illustrated in the complex plane.   The equation shown at the top right describes the circle in the complex plane. When φ = 0 the equation evaluates to zero, i.e. it's at 1 on the x-axis. When φ = π, the equation evaluates to -1 on the x-axis. So eiπ simply refers to the point (-1,0) in the plane. The mystery of the formula goes away entirely if instead of thinking of imaginary numbers we simply use (cos φ, sin φ) as the locus of the circle. When φ = 0 we get the point (1,0), when φ is π/2 we get (0,1), when φ = π we get the point (-1,0) and when φ = 3π/2 we get (0,-1). [Caption credit: Andrew Barker]

 

For any real number φ, Euler's formula is

 

     e^{i φ} = cos φ + i sin φ

 

where e is a fundamental constant (the base of natural logarithms) and i = √–1. If we now put φ = π, we get

 

     e^{i π} = cos π + i sin π,

 

and since cos π = -1 and sin π = 0, this reduces to

 

     e^{i π} = –1

 

so that

 

     e^{i π} + 1 = 0.

 

This most extraordinary equation, called Euler's identity, first emerged in Euler's Introductio, published in 1748. It is remarkable because it links the most important mathematical constants, e and π, the imaginary unit i, and the basic numbers used in counting, 0 and 1. In describing the equation to students, the Harvard mathematician Benjamin Peirce said: "Gentlemen, that is surely true, it is absolutely paradoxical; we cannot understand it, and we don't know what it means, but we have proved it, and therefore, we know it must be the truth."

 

In a letter to Mathematics Today, Dec.2005 (p. 197), Stephen Castell writes:

 

This expression underlines that it should never cease to astonish us, mathematically, that raising a transcendental to the power of another multiplied by something totally imaginary has the same value as a perfectly real number – and a negative one to boot. One might have 'expected' the value to be some other – positive – transcendental?

 

Physically, this beautiful identity links real-world ratios of key circle metrics with natural logarithms, and with the 'intrinsic exponentiality' of the growth of many physical and biological processes; and ... with the entirely 'imaginary' (dark matter?). Yet it is all grounded in an implicit statement about the eternal, recurring sinusoidality of nature itself, deriving from the identity e^ix = cos x + i sin x.

 

But ... the latest thinking in physics is that 'universal constants' (such as the speed of light), may not be 'constant' after all – they may perhaps only be examples of what I recently called datoids.^* It is therefore interesting for mathematicians to ask: does this beautiful identity still hold true in a part of the universe where (through gravitational contortions in the space-time continuum) the circle metrics give a value for π which is not 3.14159... – but, say, precisely 4.14 [and similarly for the value of e]?

 

One would suppose that the answer to that question is "No", since this would lead to the conclusion that i and/or 1 could not, in that strange region, be exactly 'integers'. Such a conclusion would present a profound mathematical / logical / philosophical problem, since the 'intrinsic' phenomenon and process of number, and (ontologically integer) counting, would be threatened – it may not even 'work' at all.

 

But why should gravitationally-twisted space-time result in the breakdown of integer and counting? Could it be, rather, that intrinsically integers themselves are also mere datoids? If so, what is the more fundamental, integral, truth of which whole numbers are only a highly-useful-on-Earth approximation? Is the 'universal' (and not necessarily constant) unit of counting actually '-e^iπ', and not '1'...?

 

^* 'Data and datoids,' Comment: Letters, Physics World, June 2005, p. 21.

 

Related category: NUMBER THEORY

 

Euler's formula for polyhedra

Euler's formula for polyhedra is the earliest known equation in topology. If F is the number of faces of a polyhedron, E the number of edges, and V the number of vertices, Euler's formula can be written as

 

    F – E + V = 2.

 

For example, the surface of a cube has six (square) faces, twelve edges, and eight vertices and, sure enough, 6 – 12 + 8 = 2. The quantity F – E + V is known as the Euler characteristic.

 

Related category: SOLIDS AND SURFACES and TOPOLOGY

 

Euler characteristic

The Euler characteristic is one of the important quantities, known as a topological invariant, that describes the shape or structure of topological space. Euler originally formulated the characteristic for polyhedra and used it to prove various theorems about them, including the classification of the Platonic solids. For the special case of polyhedra, the Euler characteristic equals 2 (see Euler's formula for polyhedra).

 

In algebraic topology, the Euler characteristic arises from homology and connects to many other invariants.

 

Related category: TOPOLOGY

 

Euler circuit

An Euler circuit is a connected graph such that starting at a vertex a, one can traverse every edge of the graph once to each of the other vertices and return to vertex a. In other words an Euler circuit is an Euler path that is a circuit. Thus, using the properties of odd and even degree vertices given in the definition of an Euler path, an Euler circuit exists if and only if every vertex of the graph has an even degree. The concept of an Euler circuit is useful in the solution of mazes.

 

Related category: GRAPHS AND GRAPH THEORY

 

Euler path

An Euler path is a path along a connected graph that connects all the vertices and that traverses every edge of the graph only once. Note that a vertex with an odd degree allows one to travel through it and return by another path at least once, while a vertex with an even degree only allows a number of traversals through, but one cannot end an Euler path at a vertex with even degree. Thus, a connected graph has an Euler path which is a circuit (an Euler circuit) if all of its vertices have even degree. A connected graph has an Euler path which is non-circuituous if it has exactly two vertices with odd degree. Compare with Hamilton path.

 

Related category: GRAPHS AND GRAPH THEORY

 

Euler square

An Euler square is a square array made by combining n objects of two types such that the first and second elements form a Latin square. Euler squares are also known as Graeco-Latin squares, Graeco-Roman squares, or Latin-Graeco squares. For many years, Euler squares were known to exist for n = 3, 4, and for every odd n except n = 3k. Euler's Graeco-Roman squares conjecture maintained that there are no Euler squares of order n = 4k + 2 for k = 1, 2, .... However, such squares were found to exist in 1959 by Bose and Shrikande, refuting the conjecture.

 

Related category: GAMES AND PUZZLES

 

Euler's conjecture

Euler's conjecture is that it always takes n terms to sum to an n-th power: two squares, three cubes, four fourth powers, and so. This hypothesis is now known to be wrong. In 1966, L. J. Lander and T. R. Parkin found the first counterexample: four fifth powers that sum to a fifth power. They showed that 275 + 845 + 1105 + 1335 = 1445. In 1988 Noam Elkies of Harvard University found a counterexample for fourth powers: 2,682,4404 + 15,365,6394 + 187,9604 = 20,615,6734. Subsequently, Roger Frye of Thinking Machines Corporation did a computer search to find the smallest example: 95,8004 + 217,5194 + 414,5604 = 422,4814.

 

Related category: NUMBER THEORY