Platonic solid
Figure 1. The five Platonic solids.
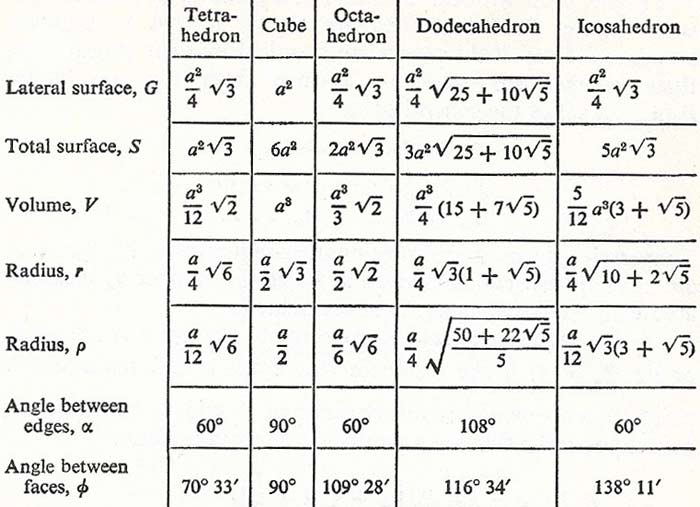
Figure 2. Measurements of Platonic solids. Notation, lateral edge a, lateral surface G, total surface S, volume V, radius of circumscribed sphere r, radius of inscribed sphere ρ, angle between edges α, and angle between faces φ.
A Platonic solid is any of the five regular polyhedrons – solids with regular polygon faces and the same number of faces meeting at each corner – that are possible in three dimensions. They are the tetrahedron (a pyramid with triangular faces), the octahedron (an eight-sided figure with triangular faces), the dodecahedron (a 12-sided figure with pentagonal faces), the icosahedron (a 20-sided figure with triangular faces), and the hexahedron or cube. They are named after Plato who described them in one of his books, though it was Euclid who proved that there are only five regular polyhedra.
A regular solid with hexagonal faces cannot exist because if it did, the sum of the angles of any three hexagonal corners that met would already equal 360°, so such an object would be planar.
General properties of Platonic solids
Let V = number of vertices, F = number of faces, E = number of edges, M = number of faces meeting at a vertex, N = number of edges and vertices associated with a face, and A = number of angles. Using Euler's formula for polyhedra, F – E + V = 2, allows us to complete the table below.
| Properties of the Platonic solids | |||||
|---|---|---|---|---|---|
| solid | M | N | F | V | E |
| tetrahedron | 3 | 3 | 4 | 4 | 6 |
| octahedron | 4 | 3 | 8 | 6 | 12 |
| icosahedron | 5 | 3 | 20 | 12 | 30 |
| hexahedron | 3 | 4 | 6 | 8 | 12 |
| dodecahedron | 3 | 5 | 12 | 20 | 30 |
Each of these solids possesses an inscribed and a circumscribed sphere, which has the same center O. Further, the mid-points of all the edges of a Platonic solid also lie on a sphere again with center O. If we construct the inscribed sphere of a Platonic solid and join neighboring points of contact of the sphere with the faces of the polyhedron, there results within the sphere another regular polyhedron, which has the same number of vertices as the original solid has faces, and the same number of edges as the original solid. The cube yields an octahedron, the icosahedron a dodecahedron, and the tetrahedron another tetrahedron.

