Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed?
– Martin Gardner

 

e is possibly the most important number in mathematics. Although pi is more familiar to the layperson, e is far more significant and ubiquitous in the higher reaches of the subject. One way to think of e is the number of dollars you would have in the bank at the end of a year if you invested $1 at the start of the year and the bank paid an annual interest rate of 100% compounded continuously. Compound interest doesn't behave in quite the way intuition suggests. Because more frequent compounding causes the principal to grow faster, it might seem that continuous compounding would make the investor very rich in short order. But the effect tails off. At the end of one year, the $1 would have grown to a mere $2.72, rounded to the nearest cent.

 

To a better approximation, e is 2.718281828459045... – its decimal expansion stretching out forever, never repeating in any permanent pattern, because e is a transcendental number. It is the base of natural logarithms, which is equivalent to the fact that the area under the curve (the integral of) y = 1/x between x = 1 and x = e is exactly equal to one unit. It also features in the exponential function y = e ^x, which is unique in that its value (y) is exactly equal to its growth rate (dy/dx in calculus notation) at every point.

 

As well as showing up in problems involving growth or decay (including compound interest) or in calculus, whenever logarithmic or exponential functions are involved, e is at the heart of the normal distribution; the shape of a hanging cable, known as a catenary; the study of the distribution of prime numbers; and Stirling's formula for approximating factorials.

 

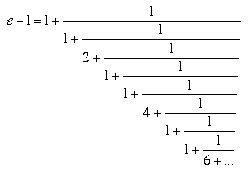
Like pi, e pops up as the limit of many continued fractions and infinite series. Leonhard Euler, who was the first to study and to use the symbol e (in 1727), found it could be expressed as the curious fraction:

 

 

No less remarkable is this infinite series of which e is the sum:

 

1 + 1/1! + 1/2! + 1/3! + 1/4! + ...

 

But of all the places that e appears in mathematics none is more extraordinary than Euler's identity from which comes the most profound relationship in mathematics: e ^{i π} + 1 = 0, linking e and π with complex numbers.

 

Reference

1. Maor, Eli. e: The Story of a Number. Princeton, NJ: Princeton University Press, 1994.