logarithm
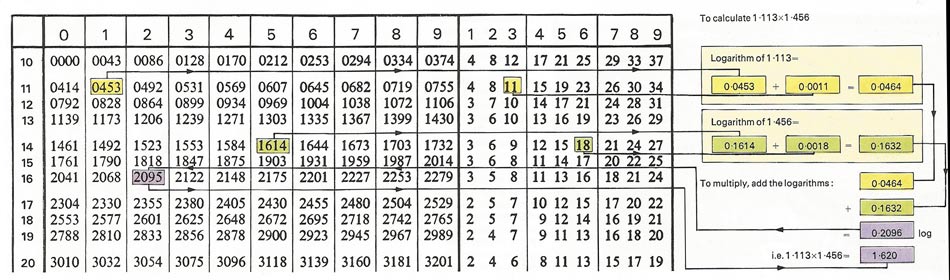
Figure 1. Log tables can be used to multiply or divide numbers.

Figure 2. The title page of the 1614 edition of Mirificia Logarithmorum Canonis Descriptio. The book discussed theorems in spherical trogonometry and introduced natural logarithms.
Log tables can be used to multiply or divide numbers. In the example illustrated in Figure 1, 1.113 is found by adding the log under 1.11 so that for 0.003, to give 0.0464. Similarly the log of 1.456 is 0.1632. The two logs are then added to give 0.2096 and the required product is the number that has this logarithm – the number 1.620 in the table. In practice, results are found by consulting tables of antilogarithms.
In Mirificia Logarithmorum Canonis Descriptio (Description of the Wonderful Rule of Logarithms), published in 1614, Scottish mathematician John Napier introduced a concept that was to explode the possibilities of research in physics, mathematics, geography, and astronomy: the logarithm (Figure 2).
Napier's name for his new mathematical figure belies its purpose: logos in Greek can be understood as "proportion", and arithmos as "number". Logarithms, then, are numbers that indicate ratios. Logarithms allow mathematicians, scientists, engineers, and navigators to perform mathematical calculations more efficiently; instead of completing manifold monotonous multiplication calculations, a researcher could employ logarithmic tables and slide rules to solve a mathematical question quickly. Mathematicians such as Henry Briggs, Nicolas Mercator, John Speidwell, and Leonhard Euler expanded upon Napier's concepts to develop the logarithmic form and rules that are still employed throughout the world in the present day.
Applications
The applications of the logarithm are far-reaching and critical. Logarithms simplify mathematics in fields such as astronomy, surveying, navigation, and physics, and so scientific discovery and innovation advanced more quickly than they might have without their aid. Researchers and practitioners continue to express ideas in logarithmic scales. For example, musical tones and intervals are expressed in logarithms, and Hick's law, which proposes a logarithmic relation between the time people take in making a choice and the number of choices they are presented with, is founded upon logarithms. Even though they might not be conscious of the exact calculations, humans use logarithmic reasoning in considering risk assessment: which issues they ought to be concerned with, and which are relative long shots. Logarithms also appear in studies of entropy, statistics, and information theory.
Mathematical description
The logarithm of a number or variable x to base b, logb x, is the exponent of b needed to give x. The bases most commonly used in mathematics are e and 10. A logarithm to base e, written as loge x or ln x, is known as a natural logarithm. (For example, loge10 is approximately 2.30258.) A logarithm to base 10 is written as log10 x and is known as a common logarithm.
Since a 0 = 1 for any a; log 1 = 0 for all bases. In order to multiply two numbers together, one uses the fact that ax.ay = ax + y, and hence log (x.y) = log x + log y. We therefore look up the values of log x and log y in logarithmic tables, add these values, and then use the tables again to find the number whose logarithm is equal to the result of the addition. Similarly, since ax/ay = ax = y = log(x/y); and since (ax)y = axy, log x y = y.log x. Logx x = 1 since x 1 = x.
To calculate in decimal numbers, logarithm tables need be compiled only for the numbers between 0 and 9.999 (in four-figure tables; in five-figure tables include 9.9999, and so on to as many figures as required). Larger numbers are expressed by adding a whole number (integer) called the characteristic, which represents in base-10 logs the corresponding power. The four-figure logarithm to the base 10 (written log10) of 2, for example, is 0.3010. The log of 200 is 2.3010 and of 2,000 is 3.3010 (200 is 102 × 100.3010 = 102.3010, and 2,000 is 103 × 100.3010 = 103.3010).
The antilogarithm of a number x is the number whose logarithm is x; that is, if log y = x, then y is the antilogarithm of x.
A logarithmic curve is the plotting of a function of the form f (x) = log x (i.e., a logarithmic function).

