slide rule

To multiply using a slide rule [A], for example to find the product of 1.5 and 4, the 1 on the upper scale is lined up with 1.5 on the lower scale. The required product is read off on the lower scale opposite the 4 on the upper – in this example to give 6. The example of division [B] is 6/3. The 3 on the upper scale is lined up with the 6 on the lower scale and the answer read off opposite the 1 on the upper scale. In this example the required answer is 2.

Close-up of part of a slide rule showing the cursor.
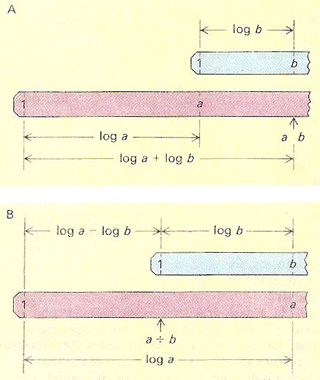
The slide rule works by the addition and subtraction of the logarithms of numbers. (A) To multiply a by b, the 1 mark on the sliding logarithmic scale (blue) is set opposite the a mark on the fixed logarithmic scale (red). The product a.b is then read off the fixed scale opposite the b mark on the sliding scale. (B) To divide a by b, the b mark on the sliding scale is set opposite the a mark on the fixed scale. The quotient a/b is then read of the fixed scale opposite the 1 mark on the sliding scale. A standard 250mm long slide rule will give answers correct to about 3 significant figures.
A cylindrical slide rule can be pictured as a set of long scales wound round the cylinder like a screw thread.
A slide rule is mechanical device based on logarithms which, before the advent of electronic calculators, was used for rapid, though approximate, calculations. Logarithmic scales are engraved on rods that can be slid in relation to each other. and numbers on them added or subtracted as needed – added for multiplication and subtracted for division. Because of the log scale, the numbers become closer together along the slide, just like the frets on a guitar's fingerboard. Unlike an ordinary ruler the scale is geometric rather than arithmetic.
History
It was the introduction of logarithm by John Napier in 1614 that made the slide rule possible. Like the logarithm, the slide rule is used to simplify tedious mathematical operations. The first adjustable logarithmic slide rule, a circular design, was created in 1622 by British mathematician William Oughtred. A typical slide rule today looks much as it did in Oughtred's time: either circular or linear, with scales for mathematical computations: multiplication, division, roots, logarithms, and trigonometry.
Slide rules continued to undergo development as technology improved and demand for detailed calculations increased. For example, improvements were made by manufacturer Matthew Boulton and by engineer James Watt for the purpose of designing steam engines, and in 1814 the physician Peter Roget (1779–1869), the Roget of thesaurus fame, invented a slide rule for calculating powers and roots of numbers. In certain fields, such as aviation, customized slide rules were required to facilitate specialised mathematical operations. The slide rule so greatly simplified what had previously take a great deal of time to calculate longhand that it is now referred to as an analog computer.
The advent of the scientific calculator made the slide rule obsolete, but slide rules offer the advantage of not relying on electricity or batteries, and they display all the operations of a calculation alongside calculations or computers, and the precision of a result can be off by as much as three significant digits, which can lead to serious error. All the same, aviators and sailers continue to carry rules in case of instrument failure. The existence of the online International Slide Rule Museum attests to the ongoing significance and utility of the instrument.
How a slide rule works
Two scales are calibrated identically so that, on each, the distance from the "1" point to any point on the scale is proportional to the logarithm of the number represented by that point. Since log (a.b) = log a + log b, the multiplication a.b can be performed by setting the "1" point of the scale (1) against a on scale (2), then reading off the number of scale (2) opposite b on scale (1). Division is performed by revering the procedure. A transparent sliding saddle called a cursor can be moved along to line up the graduations and make then easier to read.
The accuracy of a slide rule is limited mainly by its length. A cylindrical slide rule has scales up to a meter long wound round it like a screw thread. Most ordinary slide rules have several different scales for different kinds of calculations: reciprocal (a scale of all the numbers divided into 1), square (numbers multiplied by themselves), square root, and even trigonometric functions such as sine, cosine, and tangent.


