exponential
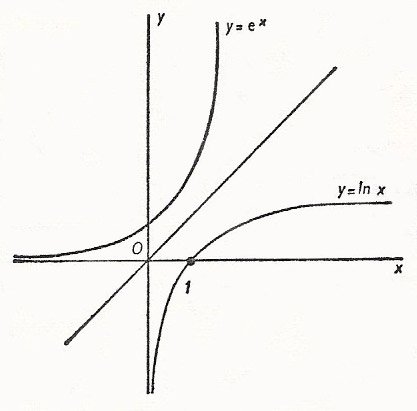
The graph of y = ex and its inverse, y = ln x.
| Who has not be amazed to learn that the function y = ex, like a phoenix rising again from its own ashes, is its own derivative? |
| – Francois le Lionnais |
An exponential is anything that grows at a rate proportional to its size. An exponential function is a function of the form y = ax, where a is an arbitrary constant greater than zero and x is variable between -∞ and +∞.
An exponential function has the property:
am . an = am + n
If a = e we have the important exponential function y = ex, where e is about 2.712... The inverse of this function is y = ln x. The exponential function to base a can be written as f (x) = ax.
It was proved by Leibniz that exponential functions are transcendental.


