Chess is a game of strategy for two players that probably originated in India, though the earliest documentary references are in Chinese and Persian texts in about AD 600. Each player has 16 pieces, either black or white, consisting of eight pawns, two rooks (also known as castles), two knights, two bishops, a queen, and a king. The object is to lay siege to the opposing king in such a way that it cannot escape attack – a position known as checkmate (from the Persian phrase "Shah Mat," meaning "the king is dead"). There is no element of chance in a game of chess and skill is the determinant of victory.

 

There are 400 first move combinations – 20 for white × 20 for black (though only 64 of these are regarded as strong), 318,979,564,000 ways of playing the first four moves, and 169,518,829,100,544,000,000,000,000,000 ways of playing the first ten moves. The total number of possible board configurations is estimated at 10¹²⁰; for comparison, that of Go is generally put at about 10¹⁷⁴.

 

A standard chessboard is a square plane divided into 64 smaller squares by straight lines at right angles. Originally, it wasn't checkered (that is, made with its rows and columns alternately of dark and light colors), and this feature was introduced merely to help the eye in actual play. In many puzzles based on chess the utility of checkering is questionable, and the board may be generalized to any n × n size.

 

Origins of chess

Chess has been attributed to some 14 different ethnic groups, although most scholars think India was its birthplace. It probably passed through Persia to Europe. Its name is from Old French, from the Hindu chaturanga, which refers to the components of an army: horses, elephants, chariots, and infantry. Its relation to warfare is seen in the Buddhist story that Buddhism invented it instead of war.

 

Chess puzzles and problems

One of the first puzzles to use a chessboard was the wheat and chessboard problem, posed in 1256 by the Arabic mathematician Ibn Kallikan. Among the earliest problems to involve chess pieces, due to Guarini di Forli in 1512, asks how two white and two black knights can be interchanged, using normal knight's moves, if they are placed at the corners of a 3 × 3 board. The unusual L-shaped movement of the knight is what makes one of the best known chess puzzles, the knight's tour, such a challenge. Other standard puzzles, often called simply the kings problem, the queens problem, the rooks problem, the bishops problem, and the knights problem, ask for the greatest number of each of these pieces that can be placed on an 8 × 8 board or on a generalized n × n board without attacking each other, and/or the smallest number of each of these pieces are needed to occupy or attack every square. Fairy chess is any variant on the standard game, which may involve a change in the form of the board, the rules of play, or the pieces used. For example, the normal rules of chess can be used but with a cylindrical or Möbius band connection of the edges.

 

Bishops problem

 

 

The bishops problem is to find the maximum number of bishops (pieces capable of moving any number of spaces along diagonals of their own color) that can be placed on an n × n chessboard in such a way that no two are attacking each other. The answer is 2n - 2, which gives the solution 14 for a standard (8 × 8) chessboard. The numbers of distinct maximal arrangements for n = 1, 2, ... bishops are 1, 4, 26, 260, 3368, ...

 

Four knights puzzle

 

On a 3 × 3 chessboard are two white knights at the top left-hand and top right-hand squares and two black knights at the bottom left-hand and bottom right-hand squares. The four knights puzzle is to exchange the black knights with the white knights in the minimum possible number of moves. One move is a normal knight's move on any vacant cell of the board, which renders the center square inaccessible.

 

Kings problem

 

 

The kings problem is the problem of determining how many non-attacking chess kings, K(n), can be placed on an n × n chessboard. For n = 8, the solution is 16. The general solution is K(n) = ¼n 2 if n is even and K(n) = ¼(n + 1)2 if n is odd. The minimum number of kings needed to attack or occupy all squares on an 8 × 8 chessboard is nine.

 

Knight's tour

 

The knight's tour is a classic chess puzzle: to find a sequence of moves by which a knight can visit each square of a chessboard exactly once. If the final position is a knight's move away from the first position, the tour is said to be closed or reentrant.

 

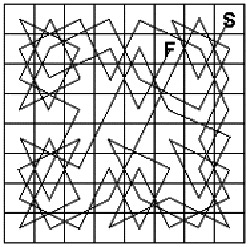The earliest known knight's tour.

 

The earliest recorded solution for a standard 8 × 8 chessboard was given by Abraham de Moivre; the earliest known reentrant solution came from the French mathematician Adrien-Marie Legendre (1752-1833). Not to be outdone Leonhard Euler found a reentrant tour that visits two halves of the board in turn. The problem can be generalized to an n × n board, with some surprising results; for example, a reentrant tour is not possible on a 4 × 4 board.

 

Magic tour

 

Suppose a chess piece makes a tour on an n × n chessboard whose squares are numbered from 1 to n² along the path of the piece. The tour is a magic tour if the resulting arrangement of numbers is a magic square, and is a semimagic tour if the resulting arrangement of numbers is a semi-magic square.

 

It was also known that such tours are possible for all boards of size 4k × 4k for k > 2. However, while a number of semimagic knight's tours were known on the usual 8 × 8 chessboard, it was not known if any fully magic tours existed on the 8 × 8 board. This long-standing open problem has now been settled in the negative by an exhaustive computer enumeration of all possibilities. The software for the computation was written by J. C. Meyrignac, and a website was established by Guenter Stertenbrink to distribute and collect results for all possible tours. After 61.40 CPU-days, corresponding to 138.25 days of computation at 1 GHz, the project was completed on August 5, 2003. In addition to netting a total of 140 distinct semimagic knight's tours, the computation demonstrated for the first time that no 8 × 8 magic knight's tour is possible.

 

Magic tours have been found in 4 × 4 × 4, 8 × 8 × 8, and 12 × 12 × 12 cubes, and on the surface of 8 × 8 × 8 cube. However, there are no known knight tours in hypercubes.

 

See Hamilton path.

 

Reference

1. Kumar, Awani. "In Search of Perfect Magic Tours of Knight on 12×12 Board." The On-line Journal for Mathematical Recreations, Issue 26, April-June 2003.

 

Queens problem

 

 

The queens problem is a famous chess problem that asks in how many ways eight queens can be placed on a chessboard so that no two attack each other. The generalized problem, to find how many ways n queens can be placed on an n × n board so that no two attack each other, was first posed by Franz Nauck in 1850. In 1874 Günther and Glaisher described methods for solving this problem based on determinants. The number of distinct solutions, not counting rotations and reflections, for board sizes of 1 × 1 to 10 × 10 is 1, 0, 0, 1, 2, 1, 6, 12, 46, and 92, respectively. The 6 × 6 puzzle, for which there is a solitary unique solution, was sold in Victorian London in the form of a wooden board with 36 holes into which pins were placed, for one penny.

 

Rooks problem

 

The rooks problem is to find the maximum number of chess rooks that can be placed on an n × n chessboard such that no rook attacks another. Since each rook attacks all squares in the rank and file upon which it rests, this number is n: the rooks may be placed along the diagonal. The total number of ways of placing n non-attacking rooks is n factorial (n!).

 

Tour

 

A tour is a sequence of moves by a chess piece on a chessboard in which each square of the board is visited exactly once.