number

Five oranges, five hens' eggs, and five bottles of wine all possess the identical property of "fiveness". The number 5, fifth along the positive real number line, can be applied to any such group of five objects. The bottles do not all have the same shape, but this obviously dos not affect their number. Only adding or removing some bottles would do that.

Keeping a tally was one of the earliest forms of counting. In this old English game called shove ha-penny the players slide coins along a board into marked-off sections. They keep their scores with chalk tally marks at the edges of the board. Ancient farmers probably counted their animals using a tally-stick, a piece of wood carved with a series of notches.

The number line is a way of representing numbers by thinking of them as the positions of points on a line.
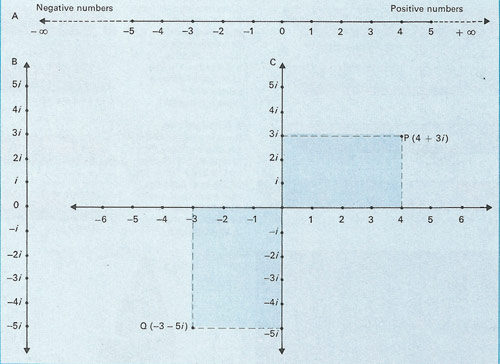
Three types of numbers are the real, imaginary, and complex numbers. Real numbers (A) can be represented as points along a line extending from minus infinity to plus infinity. They include all negative and positive numbers. Imaginary numbers (B) are based on i, the square root of –1, and can also be positive or negative. Complex numbers (C) each have a real and an imaginary part. They can be pictured as points defined by a distance along the real number axis and a distance imaginary number axis. Complex number P, for example is 4 + 3i, and Q is –3 – 5i. Complex numbers are much used by scientists.
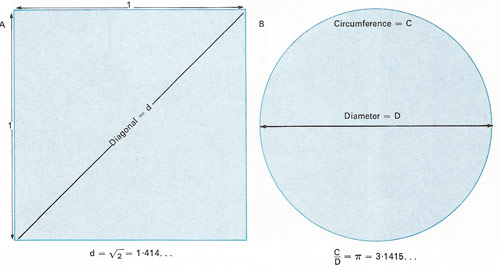
An irrational number cannot be expressed as a fraction using integers. A square with sides each one unit long [A] has a diagonal equal in length to the square root of 2. This is approximately equal to 1.414..., with a never-ending series of numbers after the decimal point. Another irrational number is the ratio of the circumference of a circle to its diameter [B], represented by the Greek letter π. It is equal to 3.1415..., again with a never-ending series of numbers after the decimal point. A rough approximation to π is given by the fraction (rational number) 22/7, which is equal to 3.142... Irrational numbers were discovered by the Greek mathematician Pythagoras.
Clock faces may have Arabic numerals [A], Roman numerals [B], or no numerals at all [C], because in a clock the numbers have come to stand merely for positions.
A number is an abstract measure of quantity. In everyday terms, numbers are usually used with units: e.g., three meters (or 3 m); 6.5893 kilograms (or 6.5893 kg).
The most familiar numbers are the natural numbers, 0, 1, 2, ..., used for counting. If negative numbers are included, the result is the integers. Ratios of integers are called rational numbers, which can be expressed as terminating or repeating decimals. If all infinite and non-repeating decimal expansions are thrown in as well, the scope of numbers extends to all real numbers, which can be extended to the complex numbers in order to include all possible solutions to algebraic equations. More recent developments are the hyperreal numbers and the surreal numbers, which extend the real numbers by adding infinitesimal and infinitely large numbers (see infinity). For measuring the size of infinite sets, the natural numbers have been generalized to the ordinal numbers and to the cardinal numbers.
All ancient cultures devised their own number systems for the practical purposes of counting and measuring. The development of the idea of place-value notation and the introduction of zero into the base-10 number system that we use today. This system seems to have reached the West from India via 12th-century translations of Arabic mathematical writings. From the basic process of counting we get the natural numbers.
See also numeral and number system.
The concept of numbers
The idea of number is a basic concept. The distinction between one and many is probably the easiest for a child to understand. A girl on a beach can pick up one pebble although she can see many more. If she picks up a handful, she obviously has more than one pebble but far less than the total number she can see. To obtain a precise idea of how many she has, she can count the number of pebbles in her hand and find, for example, that there are 12. "Twelve" is the name given to that number of pebbles It is a property possessed by all collections of 12 objects: 12 cows, 12 seagulls, and 12 books.
Positive and negative integers
Whole numbers, such as 1, 7, and 319, are called positive integers and have been used ever since humans began to count. In the Middle Ages the Hindus developed the concept of negative integers to deal with amounts owing in a trading transaction. A man might own five (+5) sheep and owe three (–3), so that he really owns only 5 – 3 = 2 sheep.
As long as mathematical operations are limited to counting, integers are sufficient as numbers. But as soon as people started to measure they found that nature is not organized into integer lengths and areas. A farmer could make a measuring stick (a ruler) by marking off a piece of wood into similar lengths equal to, say, the length of his foot. He might find that one of his animals was 5 "feet" long, whereas its offspring was only 2 "feet" long. Then he might find an animal that was 3 1/2 "feet" and another 2 1/3 "feet" He would thus discover a whole new family of numbers, called rational numbers. Any number that can be written in such a form as 8/3 – as a fraction (the ratio of two integers) – is a rational number. Such numbers can be positive or negative and all integers are rational.
In the sixth century BC Greek mathematicians discovered that a square with sides one unit long has a diagonal whose length cannot be measured exactly. No matter what scale of length is used, and no matter how finely it is subdivided into fractions, such a length cannot be measured with precision nor can it be written as a fraction. The system had to be extended again to include this new class of numbers, which are now called irrational numbers.
Today we use zero (0) to denote the absence of a number, but this has not always been so. The Roman numeral system, for instance, had no zero. It was introduced for its present role in about 600 BC by Hindu mathematicians, who formulated rules for calculating with it: multiplying by zero always gave a zero result and addition or subtraction of zero leaves a number unaltered. Hindu mathematicians also recognized that dividing by zero does not produce a result that can be defined by the number system.
Infinite and imaginary numbers
The concept that there are infinitely large numbers was first discussed by the Greek mathematician Archimedes. Starting with the largest number in the Greek number system, "a myriad myriads" (a hundred million), he constructed even larger numbers. He then estimated the number of grains of sand in the universe and showed that this was less than his largest number.
Archimedes showed that there is no upper limit to a number system. Infinity, unlike zero, is not a number. No matter how large a number is there is still an indefinite number larger than it. Infinity can never be reached.
With the concepts of zero and infinity, humans had a complete number system that could be pictured as every real number along a line stretching from minus infinity to plus infinity. But with the development of squares and square roots, mathematicians encountered such problems as: what is the square root of –5? At first such problems were thought to be impossible to solve because there is no real number which, when squared, gives a negative result. Then in the 16th century Italian mathematicians introduced the 'imaginary' quantity i which, when squared, gives the result -1. Numbers involving i are called imaginary numbers.
Complex numbers consist of a real part and an imaginary part, such as 5 + 3i. They can be manipulated in the same way as purely real numbers. Many branches of modern engineering and electronics use them.
The system of numbers commonly used today was adapted from the Arabic numbering system which, in turn, was based on Hindu ideas. In this system the position of a digit (numeral) in a number is significant. Using the basic digits 0 and 1 to 9 it is possible to construct any number. This base-10, or decimal, system was introduced into Europe by Adelard of Bath in about 1100 and by 1600 was in almost universal use.
What is the base?
The base, or radix, is the number of digits in a number system. Position is important because in a number such as 333, the first 3 stands for 300, the second for 30, and the third for 3 units. But any convenient base can be used. Modern digital computers, for example, use the base of 2 – the binary system of numbers – because its only digits, 1 and 0, can easily be represented by "on" and "off" positions of switches.

