asymptote
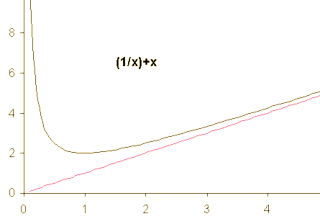
The red line (y = x) and the y-axis are both asymptotes of the curve y = 1/x + x.
If a curve is such that a straight line may be drawn which the curve approaches closer and closer without ever actually touching, then the line is called an asymptote and the curve is said to be asymptotic.
Imagine facing along the direction of a fantastically (in fact infinitely) long, straight wall that is just a meter to your right. Every second, you walk forward a meter and at the same time move sideways slightly so that you exactly halve the distance between you and the wall. The path you follow is asymptotic, and the line of the wall is an asymptote to your path.
The word "asymptote" comes from the Greek roots a (not), sum (together), and piptein (to fall), so that it literally means "not falling together;" it was originally used in a broader sense to describe any two curves that don't intersect. Proclus wrote about both asymptotic lines and symptotic lines (those that do cross). Nowadays, the term "symptotic" is hardly ever heard, and "asymptote" is used mainly to denote lines that serve as a limiting barrier for some curve as one of its parameters approaches plus or minus infinity.
The "~" symbol is often used to show that one function is asymptotic to another. For example, f (x) ~ g(x) indicates that the ratio of the functions f (x) to g(x) approaches 1 as x tends to infinity. Asymptotes are not always parallel to the x- and y-axes, as shown by the graph of x + 1/x (illustrated here), which is asymptotic to both the y-axis and the diagonal line y = x.


