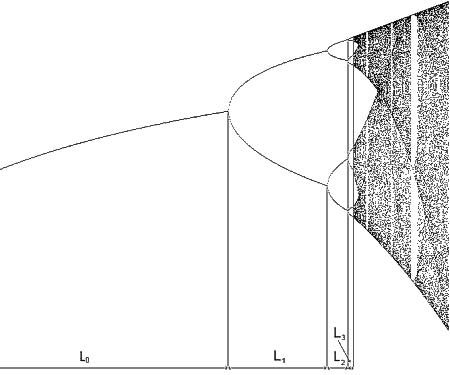
Feigenbaum's constant is a universal constant, denoted by the Greek letter, that governs the behavior of systems that are approaching chaos; it was discovered by the American mathematical physicist Mitchell Feigenbaum (1944–) in 1975 and has the value δ (delta) = 4.6692... All one-dimensional chaotic systems have a behavior, as they approach instability, known as period doubling. The Feigenbaum constant gives the rate at which the period of the system doubles.